코딩테스트용 라이브러리 정리

📜 제목으로 보기

• 표준라이브러리 6가지
  • 내장함수
  • itertools
  • heapq
  • bisect
  • collections
  • math
• 그외
  • map, split, sorted
• 주의점
  • input말고
  • 재귀풀기
  • Pypy

• 참고
  • 벨로그
  • justkode

표준라이브러리 6가지

내장함수

• sum, min, max, eval, sorted(key=, reverse=)

  result = eval("(3 + 5) * 7")
  print(result)
  

itertools

반복되는 형태의 데이터를 처리하는 기능을 제공, 순열과 조합 라이브러리르 제공

• permutations(r개의 데이터를 뽑아 나열하는 모든 경우(순열))

• combinations(r개의 데이터를 뽑아 순서를 고려하지 않고 나열하는 모든 경우(조합))

• products(r개의 데이터를 뽑아 일렬로 나열하는 모든 경우(순열)를 계산한다. 다만 원소를 중복하여 뽑는다.)

  from itertools import product
    
  data = ['A', 'B', 'C'] # 데이터 준비
  result = list(product(data, repeat=2)) # 2개를 뽑는 모든 순열 구하기(중복 허용)
    
  print(result)
  # [('A', 'A'), ('A', 'B'), ('A', 'C'), ('B', 'A'), ('B', 'B'), ('B', 'C'), ('C', 'A'), ('C', 'B'), ('C', 'C')]
  

heapq

힙을 활용한 우선순위 큐 기능을 구현할 때 사용되며, O(NlogN)에 오름차순 정렬을 제공한다. PriorityQueue 라이브러리가 따로 있지만, heapq가 더 빠르게 동작한다.

• PriorityQueue를 리스트나 힙으로 구현할 수 있지만
  • 리스트는 삽입 O(1) 삭제 O(N) 의 복잡도를 가지지만,
  • 힙은 삽입 O(logN) 삭제 O(logN) 의 복잡도를 가진다.
    • 그래서 우선순위 큐는 보통 힙으로 구현하고, 시간복잡도도 힙으로 구현한 시간복잡도를 사용한다.
• heapq.heappush() : 원소 삽입
• heapq.heappop() : 원소 꺼내기
• heapq.heapify()

import heapq

def heapsort(iterable):
	h = []
    result = []
    # 모든 원소를 차례대로 힙에 삽입
    for value in iterable:
    	heapq.heappush(h, value)
    # 힙에 삽입된 모든 원소를 차례대로 꺼내어 담기
    for i in range(len(h)):
        result.append(heapq.heappop(h))
    return result
    
result = heapsort([1, 3, 5, 7, 9, 2, 4, 6, 8, 0])
print(result)
# [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

• 히피파이를 이용한 힙정렬
  • 기존에 있는 list 객체로 힙 정렬 만들기

import heapq

h = [3, 9, 1, 4, 2]
heapq.heapify(h)	# 파라미터로 list 객체를 받는다.

for _ in range(6):
	print(-heapq.heappop(h))	# 작은 값부터 출력된다.

bisect

• 이진 탐색을 쉽게 구현할 수 있도록 bisect 라이브러리를 제공함. ‘정렬된 배열’에서 특정한 원소를 찾아야 할 때 매우 효과적이다. O(logN)에 정렬된 배열에 맞는 위치를 찾아준다.
• ‘정렬된 리스트’에서 특정 범위에 속하는 원소의 개수를 구하는데 효과적이다.
  • bisect_left(a, x) : 정렬된 순서를 유지하면서 리스트 a에서 데이터 x를 삽입할 가장 왼쪽 인덱스를 찾는 메서드
  • bisect_right(a, x) : 정렬된 순서를 유지하면서 리스트 a에서 데이터 x를 삽입할 가장 오른쪽 인덱스를 찾는 메서드
• bisect 모듈은 이미 정렬되어 있는 list의 정렬 상태를 유지하기 위해 사용되는 모듈입니다. 이를 이용해서, 기존에 있는 list의 정렬 상태를 유지 할 수 있고, 이를 응용해서 Binary Search 또한 구현할 수 있습니다.

from bisect import bisect_left, bisect_right

a = [1, 2, 4, 4, 8]
x = 4

print(bisect_left(a, x)) # 2
print(bisect_right(a, x)) # 4

정렬된 리스트’에서 특정 범위(시작과 끝)에 속하는 원소의 개수를 구하는데 효과적이다.

• left는 같아도 젤 왼쪽 index(포함), right는 같아도 젤 오른쪽index(미포함, 들어가야하는 자리)를 반환하므로 시작과 끝 index를 알 수 있다.

from bisect import bisect_left, bisect_right

# 값이 [left_value, right_value]인 데이터의 개수를 반환하는 함수
def count_by_range(a, left_value, right_value):
    right_index = bisect_right(a, right_value)
    left_index = bissect_left(a, left_value)
    return right_index - left_index
    
# 리스트 선언
a = [1, 2, 3, 3, 3, 3, 4, 4, 8, 9]

# 값이 4인 데이터 개수 출력
print(count_by_range(a, 4, 4)) # 2

# 값이 [-1, 3] 범위에 있는 데이터 개수 출력
print(count_by_range(a, -1, 3)) # 6

• lgN으로 정렬까지 해주는 bisect.insort( )도 있다.

• bisect 모듈은 이미 정렬되어 있는 list의 정렬 상태를 유지하기 위해 사용되는 모듈입니다. 이를 이용해서, 기존에 있는 list의 정렬 상태를 유지 할 수 있고, 이를 응용해서 Binary Search 또한 구현할 수 있습니다.

# 1. 삽입 되어야 하는 index 찾기

import bisect
arr = [1, 2, 3, 3, 4, 5]

print(bisect.bisect_left(arr, 6))   # 6이 들어가야 하는 Index인 6을 반환
print(bisect.bisect_right(arr, 6))  # arr에 6이 없기 때문에 위와 똑같은 값을 반환한다.

print(bisect.bisect_left(arr, 3))   # 중복 되는 값 제일 왼쪽, 2를 반환한다.
print(bisect.bisect_right(arr, 3))  # 중복 되는 값 제일 오른쪽 + 1, 4를 반환한다.

bisect.insort_left(arr, 3)  # 중복 되는 값 왼쪽에 삽입
bisect.insort_right(arr, 3) # 중복 되는 값 오른쪽에 삽입

print(arr)

#2. Binary Search 구현
from bisect import bisect_left 
arr = [1, 2, 3, 3, 4, 5]
  
def bs(arr, x): 
    i = bisect_left(arr, x)             # 들어가야 하는 '제일 왼쪽' index 반환
    if i != len(arr) and arr[i] == x:   # 들어가야 하는 index가
        return i                        # 마지막 index + 1 이라면, arr에 x가 없는 것
    else:                               # arr[i] == x가 아니라면, arr에 x가 없는 것
        return -1
  
a  = [1, 2, 4, 4, 8] 
x = 4
res = bs(a, x)
if res == -1: 
    print(x, "는 없습니다!") 
else: 
    print("첫번째", x, "가 등장한 위치는", res) 

collections

덱(deque), 카운터(Counter) 등의 유용한 자료구조를 포함하고 있는 라이브러리

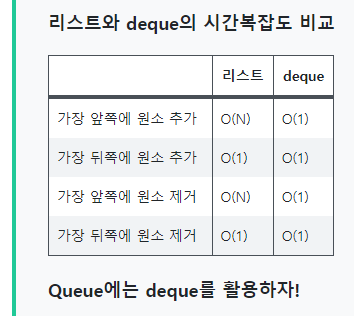
• deque

  • 파이썬에서는 일반적으로 deque를 활용해 큐를 구현한다.
  • Queue 라이브러리 있지만 일반적인 큐 자료구조를 구현하는 라이브러리는 아니다.
  • 리스트와 다르게 인덱싱, 슬라이싱 등의 기능은 사용할 수 없다.
  • 데이터의 시작이나 끝부분에 데이터를 삽입하는데 효과적이다.

  

• Counter 등장 횟수를 세는 기능을 제공한다. iterable 객체가 주어졌을 때, 해당 객체 내부 원소가 몇 번 등장했는지 알려준다.

math

수학적 기능을 제공하는 라이브러리

자주 사용되는 수학적인 기능을 포함하고 있는 라이브러리 팩토리얼, 제곱근, 최대공약수(GCD) 등을 계산해주는 기능을 포함

• 종류
  • math.factorial() : 팩토리얼
  • math.sqrt() : 제곱근
  • math.gcd() : 최대공약수
  • math.pi : 파이
  • math.e : 자연상수

import math

print(math.factorial(5)) # 120

print(math.sqrt(7)) # 2.6457513110645907

print(math.gcd(21, 14)) # 7

print(math.pi) # 3.141592653589793

print(math.e) # 2.718281828459045

그외

map, split, sorted

주의점

input말고

• 뭐 어느정도로 더 빠르고 느리냐는, 코딩 테스트 문제푸는 수준에서 다룰만한 내용이 아니므로 넘어가도록 하고, 직관적으로만 느꼈던 것은, input() 으로 코드를 제출할 시, 시간초과가 뜨지만, sys.stdin.readline() 으로 제출할 시 정답이 뜨더라는 것이다. 이와 비슷한 이슈는 이미 이전부터 있었다.

한편, 나는 입출력을 지금까지 이런 방식으로 했다.

a = [int(x) for x in input().split()]  
# a = [1, 2, 3, 4 ,5]

하지만, 이 방법보다 다음 방법이 더 권장된다. (위와 같은 이유로)

import sys  a = list(map(int, sys.stdin.readline().split()))# a = [1, 2, 3, 4, 5]

재귀풀기

• 이전에 문제풀다가 말한 적이 있는데, 특히 자주접하는 DFS, BFS 문제의 경우 그렇다.

  파이썬의 재귀 허용 깊이의 기본치가 c 보다 약한건지, c 로 짠 DFS, BFS의 경우 문제 없이 돌아가지만, 파이썬으로 돌리면 런타임 오류가 뜨는 경우가 있다. 그래서 다음과 같이 재귀 허용 깊이를 수동으로 늘려주는 코드를, 코드 상단에 적어줘야 한다.

  import sys  sys.setrecursionlimit(10**8) # 10^8 까지 늘림.
  

Pypy

• PyPy 가 뭔지 찾아보니, 쉽게말해 파이썬 보다 몇 배 더 빠른 개선된 파이썬이라고 생각하면 된다.

  좀 더 자세히 말하면, Python3 는 내부적으로는 C로 짜여져있는데 (이 이유 때문에 Python2 보다 빠르다.), 이를 C가 아니라 Python으로 다시 짠 것이다. 당연히 느릴 것 같은데, 의외로 빠르단다. 자세한 내용은 나무위키 참고.

  때문에, 일반적으로 Python3 보다 PyPy로 제출해서 내는게 더 안전한 듯 하다. (빠르다는 의미에서)

  한편, PyPy에서는 sys.setrecursionlimit(10**8) 이 안먹는다. 즉 임의로 재귀 호출 깊이를 설정할 수 없다는 것에 주의해야 한다.

  파이썬으로 문제푸는 게 편한점도 많지만 아직 어색하고, 이런 자잘한 리스크가 많은 듯 하다. 이후 또 뭔가 발견하면 남겨놔야겠다.