📜 제목으로 보기

알고리즘 푸는 이유

  1. 구현: 생각하는 내용을 코드로 옮긴다. 연습안하면 안된다. 500문제 이상 풀어야함. 반복해야 언제 어떤 변수를 선언하고 언제 전처리 해야하는지 알 수 있게 된다. 빨라지고 나만의 코딩스타일이 생긴다.
  2. 효율성: 계속 구현하다보면, 효율성을 챙기면서,
    • 자주 사용하는 함수로 최적화
    • 다른 사람들의 코드를 보면서, 효율적인 코드 작성
  3. 절차적 사고: 절차적인 사고에 익숙해짐.
    • 언제 어떤 과정을 하고, 다음은 어떻게 해야하는지
    • 적재적소한 알고리즘을 선택할 수 있게 된다.
      • 그럴려면 자료구조, 알고리즘을 따로 공부해야한다.
  4. 디버깅: 한번만에 맞는 경우는 거의 없다.
    • 예외케이스 탐색을 많이 해야한다.
      • 최저, 최대, 최악 경우를 넣어보면서 한다.
      • 코드(에러)를 읽는 능력
  5. 재미:
    • 적은시간으로 연습 가능
    • 프로젝트와 다르게 짧은 주기로 성취감

문제보고 감잡기

  1. 1초당 가능한 복잡도 간 미리 계산하기

    • python으로

      • 백만번(10^6) 반복문or덧셈곱셈 등… -> 1초 안에 다 풀린다.
      • 천만번(10^7) -> 1초 안에 대부분 풀린다.
        • python으로 1초안에 천만~5천만(10^7 ~ 5* 10^7)까지 연산 가능하다 생각하자.
      • 1억(10^8) -> 불가능 -> 알고리즘 바꿔야함.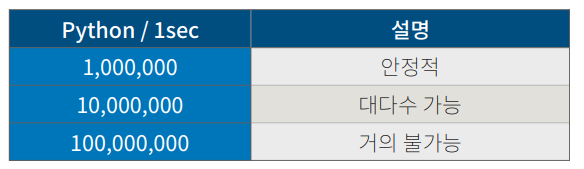 image-20211025173359400

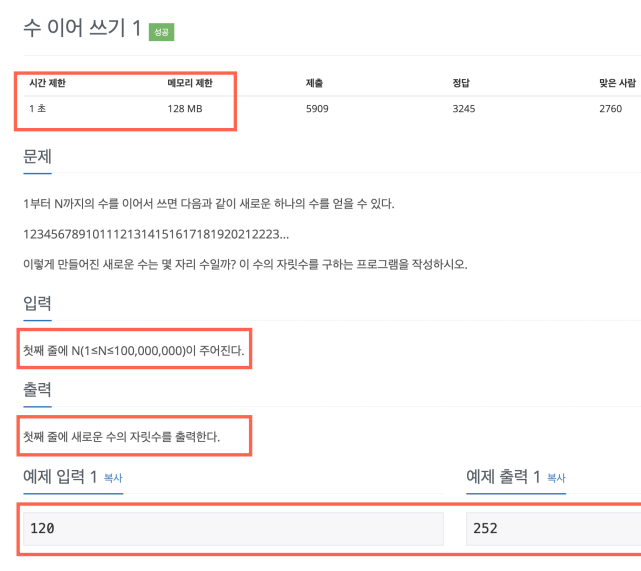
    • 다시 문제보기 image-20211025173951186

      • 시간제한부터 보기

        • 1초 -> 10&7 안에 풀어야한다.

      • 입력 보고, 반복문 횟수 갸늠하기

        • n = 10억 = 10^9 -> 단순 반복문 O(N)으로 는 불가능하다.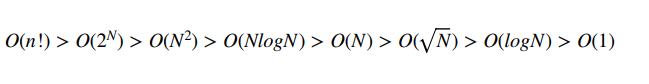 image-20211025174009251
        • 입력을 보고 O(N)이상 불가 -> 루트(n) or lgN or O(1)으로 해야한다.

PS팁

  1. 입력과 초기화

    • python의 input은 3가지 종류를 받는다.

      • 숫자1개

        • python에서는 항상 string으로 들어온형변환부터 해준다.

        image-20211025204602247

      • 문자열

        • 일반 문장
        • 쪼개면서, [i]번째 인덱싱도 하고 싶다 -> list()
          • immutable한 string 대신 list로 변환시켜줘야한다.
        • 다시 붙일려면 ”“.join사용

        image-20211025204613631

      • 숫자 배열

        • map을 써서 형변환한다.

        image-20211025204621793

    • **list(배열)의 초기화는 comprehension으로 **

      image-20211025204933684

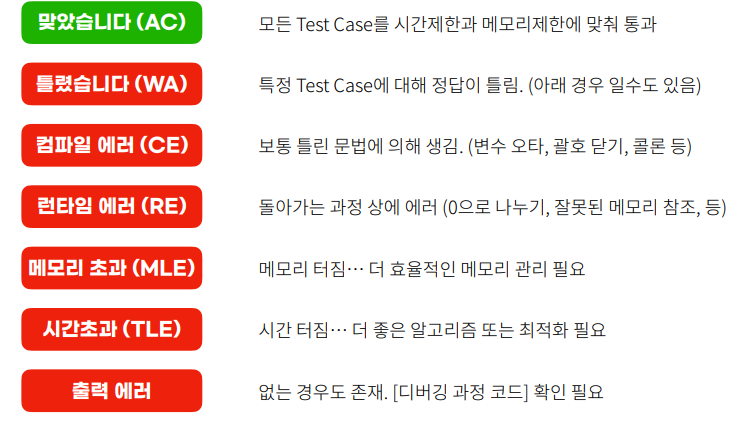
  2. 에러메세지 확인하기
    • RE: 런타임에러 -> zerodivision or indexError
    • TLE: 시간초과 -> 잘짰는데 무한루프가 있거나, 알고리즘이 안 좋거나 image-20211025205503707

  3. 추상화와 기능분리

    • 맨 처음 반복문에 돌아가면서 기능을 해줄 or 테케마다 처리해줄 input()받기부터 시작하는 함수를 짜자. 대충 로직을 슈도코드 짜듯이 짜면서 반복문 - 체크 - 결과값 저장 등의 로직을 짠다.

    • 코딩하는 2가지 방법

      • 현재가 main함수라고 가정하고 while 문에서 다 돌리기
      • process함수를 따로 만들어놓고, 테케를 process함수에서 받아 main에서 돌림

    • 처음에는 다 while문에 넣고 돌린다. image-20211025205759579

    • 하지만, main함수는 최소화 해서 가벼워야한다. 내용들은 다 함수로 보낸다.

      • 반복문을 돌되, 각 TestCase마다 따로 처리되도록 함수로, TC별 처리되도록 하는 함수를 만들어서 돌린다.

      image-20211025205932783

      • 일단 위에 스샷기준으로는..
        • 테케별 처리도되록 함수에서 input을 받고 -> 리하고 -> return 하고-> main에서 for문 print(함수return값)

    • 예를 들어, 삼성기출-사다리조작문제를 보자. (풀이는 안함)

      1. 삼성쪽은 문제가 되게 길다. 그림 위 수치 위주로 빠르게 한번 보자.

        • 일단 수치(숫자)를 먼저보고 "아~ 사다리가 5줄, 6줄 되는 구나 "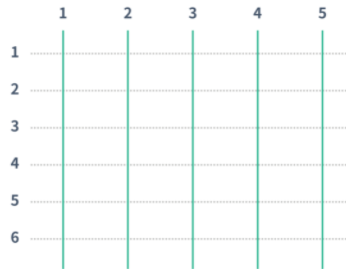 image-20211025212129731

        • 사다리를 중간에 넣을 수 있구나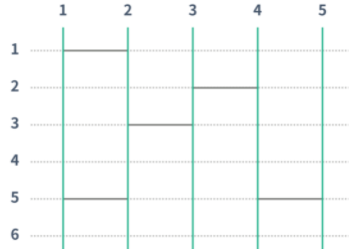 image-20211025212154704

        • 사다리를 진행해나가는 과정이 있구나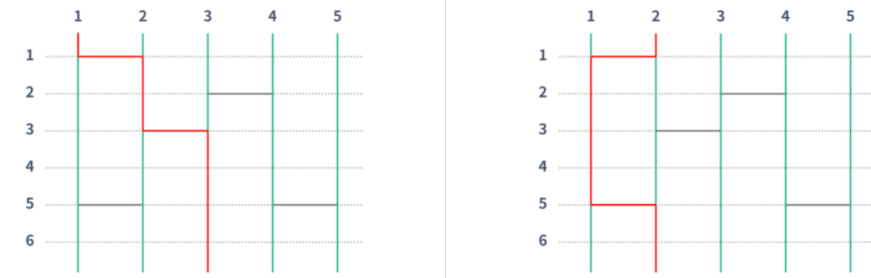

          image-20211025212234097

      2. 입력 양식(예제 입력)보기

        • 첫줄의 숫자와, 나머지 아래 숫자가 같으니까 아 대충 아래쪽이 사다리를 의미하겠구나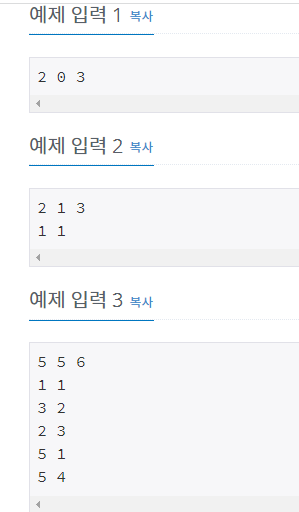 image-20211025212347073

      3. 문제를 자세히 읽기 시작하는데 출력 요구사항을 먼저 본다 image-20211025212431718

      4. 문제가 복잡해보인다.

        • **이 때, main함수를 간단하게 만들기 위해, 반복문 어떻게 돌릴지 판단 -> 그안에서 사용될 기능 분리하여 일단 슈도코드로 함수들을 작성해 기능분리 시켜준다. **

        • 사다리를 최대3개까지 놓는데,

          • i에 놓을지

            j에 놓을지

            k에 놓을지 선택할 수 있게 3중for문을 만들어 탐색가능하게 함.

          • 3개에 따라 가능한지 확인하는 check(i,j,k) 함수를 사용하고 슈도코드로 위에다 작성해둔다.

          • 가능할 때, 그 i번째 사다리가 i로 내려오는지 체크해주는 함수result()도 슈도코드로 작성해둔다.

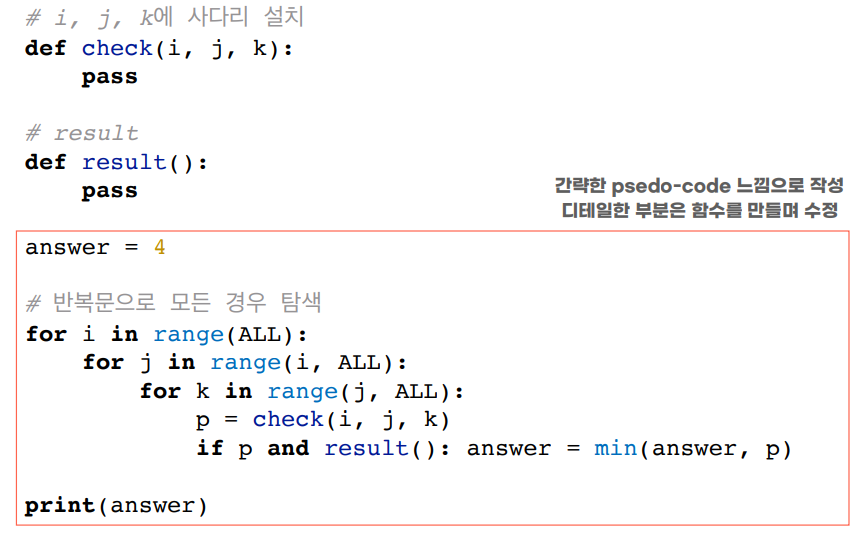
          image-20211025212604856 image-20211025212618150

  4. 코드를 줄여 가독성을 높이는 조건문, 반복문, 함수 by python indent를 줄이기

    1. 반복문 eX> N by N by N 3중 포문 image-20211025213501612

      • 똑같이 N**3 만큼 횟수는 동일하게 돌아가는데, 한번에 for num in range(N**3)으로 돌리면서

        • i = num을 N^2으로 나눈 몫 = num // (N*N)
        • j = num을 N으로 나눈 몫을, 다시 N으로 나눈 나머지 = num//N % N
        • k = num을 N으로 나눈 나머지 = num % N

      • **내가 만든 2중 포문을 indent 1개로 **

        • i = num을 N으로 나눈 몫
          • N*N을 통해, ` 0~N-1을 첫번째 구간으로해서 N개` 존재하는데,
            • 0~N-1구간: 행을 0으로 간주해요
            • N~2N-1 : 행을 1로 간주해요
            • …
            • ~N^2-1 N개의 구간이 있어요
        • j = num을 N으로 나눈 나머지
          • 구간별로 0~N-1의 열을 담당해요.
        for num in range(N**2):
    i, j = num//N, num%N
    print(f"({i},{j})" , end = " ")

      • 진법, 진수를 활용하면 더 쉬워진다고 한다.

    2. main 반복문 속 조건문을 if True:시 process()가 아니라 if not False시: continue로 아래 process() 건너띄기를 통해 indent를 챙길 수 있다.

      image-20211025215821652

      • process()함수 위에다가 if not 조건문 :continue를 활용해서 탈락시 건너띄기하면, 반복문내 indent를 줄일 수 있다.

    3. 함수안에 if : return 다음에는 else가 필요없다.

      • **if return / return도 return 삼항연산자로 줄일 수 있다. **
        • 가장 선호. flag도 이런식으로 할 수 있다.

      image-20211025220112911

  5. 변수명은 snake_case로, 함수명은 cameCase로, Pascal은 시작부터 대문자인 Camel

  6. 적용해보기 주사위네개

    • 나는 Counter를 활용했지만..
    # 기존 내코드
N = int(input())
   
from collections import Counter
   
max_money = float('-inf')
# 같은 눈이 4개가 나오면 50,000원+(같은 눈)×5,000원의 상금을 받게 된다. 
# 같은 눈이 3개만 나오면 10,000원+(3개가 나온 눈)×1,000원의 상금을 받게 된다. 
# 같은 눈이 2개씩 두 쌍이 나오는 경우에는 2,000원+(2개가 나온 눈)×500원+(또 다른 2개가 나온 눈)×500원의 상금을 받게 된다.
# 같은 눈이 2개만 나오는 경우에는 1,000원+(같은 눈)×100원의 상금을 받게 된다. 
# 모두 다른 눈이 나오는 경우에는 (그 중 가장 큰 눈)×100원의 상금을 받게 된다.  
   
def calc_money(data):
    max_cnt = max(data.values())
    val_lst = [ x[0] for x in data.items() if x[1]==max_cnt]
       
    if max_cnt == 4:
        return 50000 + (val_lst[0]*5000)
    elif max_cnt == 3:
        # val_lst = [ x[0] for x in data.items() if x[1]==max_cnt]
        return 10000 + (val_lst[0]*1000)
    elif max_cnt == 2:
        # val_lst = [ x[0] for x in data.items() if x[1]==max_cnt]
        if len(val_lst) == 2:
            return 2000+(val_lst[0]*500) + (val_lst[1]*500) 
        else:
            return 1000 + (val_lst[0]*100)
    else:
        return max(data.keys())*100
   
   
   
for _ in range(N):
    data = list(map(int, input().split()))
    data = Counter(data)
   
    money = calc_money(data)
   
    max_money = max(max_money, money)
   
print(max_money)

    • 수학을 이용하면서

      • 기능분리 by 함수
      • 입력과 초기화 by 튜플, 컴프리헨션
      • 반복문, 조건문 줄이기 by 한번에돌기+ if reutrn후에는 no else noelif + 삼항연산자

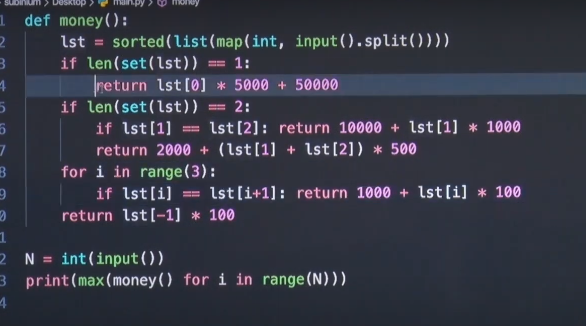
      image-20211025222302250

수학

  1. 반복문을

    • range(min(a,b))로 길이를 줄이거나
    • range(min(a,b),,-1)로 거꾸로 시작하거나
    • range(,,n)으로 간격을 주는 것을 생각하자.

  2. 유호제법은 코드로 외우자.

    • math.gcd써도될듯..
    # a>b
def gcd(a,b):
    # 1) b가 a의 약수면.. 그냥 b가 최대 공약수
    # 2) 그게 아니라면, 재귀로서 gcd(b, a%b)로 재귀로 빨리 구하자.
    return b if a%b==0 else:gcd(b, a%b)

  3. 소수판별과 에라토스테네스의 체

    • 소수판별 isPrime은

      • 이론상 소수=1과 자기자신만을 약수로 가짐 = 2~n-1까지 약수없음, 약수 나오면 탈락인데

        • 약수와 배수의 관계에서 약수는 항상 짝을 이루어 존재하니 2~루트(n)까지만 검사한다.

        image-20211026170026159

    • 에라토스테네스의 체

      • 범위가 주어진다 1~n까지 중 소스의 갯수는?
        • 1은 소수가 아니여서 지움
        • 2부터 isPrime으로 소수판별
          • 소수로 판별되면 -> 소수의 배수들을 싹다 지움(어떤수의 배수는.. 소수가 아님 무조건 x2, x3들이 약수가 되니까

      image-20211026170342838

      • 뭔가를 지울 때는 chk, ck배열에다가 index - T/F를 hashing하여 활용한다. 이미 범위가 정해져있으면 거의 이렇게 사용한다.
        • count 정렬
        • 에라토스 테네스의 체
        • DFS BFS?

      image-20211026170702162

      • 그외 자세히 주석으로 달음

        def era(N):
    # 체크는 hasing용으로서, n index를 쓸 거기때문에 0부터 시작했더라도 range(N+1)까지 돌려준다.
    ck = [ False for _ in range(N+1) ] 
    p = []
    # 1은 소수가 아니므로 제끼고 2부터 체크한다.
    # 소수의 배수들을 True를 채워놓고, 다음에 올 때 건너뛰게 한다.
    # 과거에서 판단한 소수의 배수들에 안걸렸으면, 아직 False로 남아있는, 소수는 바로 append해 줘도 된다.
    # -> 맨처음 2만, 최초이기 때문에 과거에서 True로 소수탈락시킨 경험이 없다.
    for i in range(2, N+1):
        # 아직 False인 것만 체크한다.
        # 아래에서, 미래원소들 중에 소수라고 판별내어놨으면 건너뛴다.
        # -> check를 활용해서 건너뛰는 [ck 미래 -> continue 로직]이다.
        if ck[i] == True:
            continue
        # False = 2의 배수부터 시작해서, 소수탈락(True)에 안걸렸다면, 소수라고 판단한다.
        p.append(i) 
        # 현재 i는 소수라는 뜻인데, 소수-> 소수의 배수를 True(소수탈락)로 지워야한다.
        # * i배수 조작-> i배수는 range(시작수, 끝수, i)를 통해 +i씩 움직인다.
        # 이 때, i+i or i*2부터  +i씩 i*3, i*4를 지워나가는게 아니라 
        # * < ixi >부터 시작해서 i의 배수를  지워나간다  range(i*i, N+1, i) 
        # -> 왜냐하면, 이미 과거에서 지워났기 때문인데 
        # -> 예를 들어, 6은.. 이미 2에서 지워놨음. 3에서 지울 필요X.
        # -> 3은 뭐부터 지워나가야할까? -> 앞에서 안나왔을, 3의배수로서만 존재하는, 
        # -> 3만을 약수로 가지는 = 9부터 지워나가면 된다.
        # -> 2*i부터 지눠나가도 괜찮다.
        # for j in range(i*2, N+1, i):
        for j in range(i*i, N+1, i):
            ck[j] = True 
       
    # 이제 리얼소수는 p 배열에, 체크여부는 ck(소수탈락시True?)로 반환한다.
    return ck, p
       
       
print(era(10))
# ([False, False, False, False, True, False, True, False, True, True, True], [2, 3, 5, 7])

  4. 하노이 = 분할정복 by 재귀

    • n번째 자체처리를 잘 넣어주자.
    • 재귀가 꼭 return해줄 필요는 없다. return안한다면 꼭 + 등의 연산으로 연결해줄 필요가 없다.
      • 갯수: return f(n-1) * 2 +1
      • 출력: f(n-1) + print(n자체) + f(n-1)
        • f(n-1)내부에서도 print가 호출됨.
      • BUT 재귀함수의 base case if는 반드시 return으로 종료시켜줘야한다!!
    • 변하는 것들을 인자로 잘 넣어주자. 숫자 명칭이 고정이라면, 합이 일정한 것도 이용하자.
    # 1->3def hanoi(st, ed, n):    if n==1:        return print(st,ed)    # 1->2 n-1    # st->mid     hanoi(st, 6-(st+ed), n-1)    # 1->3    print(st, ed)    # 2->3 n-1    # mid ->ed    hanoi(6-(st+ed), ed, n-1)

정렬

  1. 선택정렬(i+1~n-1와 비교 최소값 찾으면 swap, 매번 맨왼쪽 최소값 확정), 버블정렬( 매번 인접한수 비교후 크면 오른쪽으로 swap, 매번 맨오른쪽 최대값 확정)은 n, n-1, .. 1번 모두 탐색해야해서 시복 O( n(n+1)/2) = O(N^2)으로 너무 느리다.

  2. 퀵 소트

    • 재귀로 구현. 1)p정하고 2) 작, 큰그룹나눠서 3)p자리 확정의 과정을 작은그룹에서 1번, 큰그룹에서 1번 다시 시행한다.

      def quick_sort(array):
    # 리스트가 하나 이하의 원소만을 담고 있다면 종료
    if len(array) <= 1:
        return array
     
    pivot = array[0] # 피벗은 첫 번째 원소
    tail = array[1:] # 피벗을 제외한 리스트
     
    left_side = [x for x in tail if x <= pivot] # 분할된 왼쪽 부분
    right_side = [x for x in tail if x > pivot] # 분할된 오른쪽 부분
     
    return quick_sort(left_side) + [pivot] + quick_sort(right_side)

  3. 머지 소트

    • 재귀시, divide후 conquer과정에 투포인터 개념으로 merge를 해야한다.

    • 1)절반으로 나누고, 2) 각각을 투포인터개념으로 합친다.

      # 합병정렬에서는 conquer과정이 복잡하다.
# [divide] 는 그냥 반씩 쪼개면 되지만, 
# [conquer]된(정렬된 list2개) 것들을 [combine](2개 list 합하여 정렬)시 복잡하기 때문에 이 부분을 merge함수로 뺀다.
def merge(list1, list2):
    merged_list = []
    i = 0
    j = 0
    while i < len(list1) and j < len(list2):
        if list1[i] < list2[j]:
            merged_list.append(list1[i])
            i+=1 
        else:
            merged_list.append(list2[j])
            j+=1 
     
    if i == len(list1):
        merged_list += list2[j:]
    elif j == len(list2):
        merged_list += list1[i:]
    return merged_list
     
def merge_sort(my_list):
    # base case 
    if len(my_list) < 2:
        return my_list
    # divide and conquer
    left_half = my_list[:len(my_list)//2]
    right_half = my_list[len(my_list)//2:]
    # 부분문제는  원래함수(부분)을 한 상태가.. 정복된 상태다 조심!
    return merge(merge_sort(left_half), merge_sort(right_half))
     
print(merge_sort([12, 13, 11, 14, 10]))
      • 2개의 배열을 merge할 때, 4개짜리 배열을 미리 대기시켜놓고, 투포인터로 넣어줘야한다.
      • 즉, 메모리할당이 많아진다.
      • 머지 소트는 정렬 문제에서 메모리가 넉넉할 때 쓴다.
      • 퀵 소트는, 최악(역순정렬&p를 맨첫값)의 경우 NN이 될 수도 있다.

    • python sort(), sorted()는 퀵소트, 머지소트보다 더 최적화된 정렬을 쓰니. 그냥 이걸 쓰자.

  4. 라딕스 소트(radix sort) = 카운팅정렬 -> 이범정(10^6~10^7 이하)일 때

    1. **이미 최소~최대값의 범위가 정해져있을 때 **, 그 범위를 index로 hashing시킨 배열을 미리 만들어놓고

    2. 카운팅한다.

    3. 카운팅수만큼 연속해서 나열�

자료구조

  • 쓰는이유:
    • 효율성. 쓰는 의미가 있음. 사용처가 정해져있다. 메모리를 효율적으로 쓴다.
      • ex> stack: undo 마지막에 했던 작업을 되돌리기 위해. 직전꺼를 되돌리기
    • 추상적: 코드가 정해져있지 않음. 개념이므로 라이브러리가 아니더라도 어느 언어라도 구현가능해야한다.
    • 재사용성: 계속 쓰기 위해 라이브러리를 제공함
      • python은 collections에 많음.
  • stack
    • 접시닦고 다시 가져가는 것에 비유 많이함. undo
    • 넣고push 위에서부터 빼는pop 2가지가 핵심
    • 배열과 다른점은, 맨 마지막이 빠져나가는 점 : LIFO
    • python에서는 따로 library없고 배열[]로 바로 사용한다.
    • 예제 : 괄호 -> 여는괄호만 넣어서 쌓으며, 닫괄시.. 직전에 넣은 여괄 부터 꺼내 짝이 맞나 확인해야한다.
  • queue와 deque
    • 왜쓸까? 배열이랑 달라보이지만, 불필요 메모리를 줄인다.메모리를 효율적으로사용하기 위해
      • 배열로도 구현가능(pop한 앞부분으로 index를 한칸씩 당긴다.?)
      • 이미 pop한 것들을 붙잡을 이유가 없어서 그럴필요가 없음.
    • server에서 여러 queue를 써서, 여유로운 queue에 task를 넣어주는 형식(task분할)
    • python에서는 deque = stack + queue라서 queue문제는 deque
    • 예제: 요세푸스
      • 돌면서 제거된 사람을 빼야하는 경우 -> deque의 queue로 popleft + append를 rotate로 해결

그래프와 Tree의 저장방법

  • 그래프의 특이한 형태로서, 나가는 간선(outdegree)만 있으면 Tree

    • Tree도 2가지 저장방법이 있다.

      • 자식마다 부모는 only 1개씩, 자식배열에 저장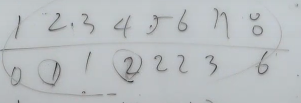 image-20211101175529986
        • cycle없이 root node제외하고 다 부모가 1개씩 존재
        • 밑에서부터 부모를 찾아 올라갈 수 있다.
          • 4의 부모 2 -> 2의부모 1 -> 1의 부모 0 == root
      • 부모마다 여러개자식을, 자식list로 2차원배열에 저장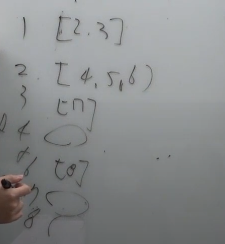 image-20211027180313109
        • 인접리스트 저장시, 아래로 내려가면서 순환을 돌기 좋다.
          • 1의 자식2 -> 2는 아래로 4,5,6을 볼 수 있으니 4번 부터 본다. -> 4번은 비어서 leaf node로 끝났따 -> 5번 보고 6번보고 하자.

    • Tree의 부모저장배열 -> LCA찾기 예시가 촌수문제다.

      • 조상들 모을 default 0의 N+1개짜리 부모저장배열 생성
        • 입력정보를 배열에 저장함. 부모 없으면 0
      • 2개 node의 공통조상찾는다?
        • 각각의 (조상, 촌수) 튜플이 담길 list를 선언
        • 한번 타고올라갈때마다 거리를 더해줄 각각의 촌수변수 선언
      • 각 node마다 부모가 없을 때까지 찾아가야한다.
        • default 0이며, 안쓰는 p[0]에 0이 들어가있어 무한루프의 가능성이 있으니, 부모가 0되는 순간 빠져나와서, 아직 처리안된상태로 나와, 마지막에 한번더 처리해준다.
        • 나부터 시작, 거리0으로서 튜플로(조상,거리)를 모아준다.
        • 재귀적으로 한번 찾아갈때마다 B = p[B] 로서, 나를 부모로 업데이트해준다. 그러면 나의 부모의 부모를 찾아가도록 된다.
      N = int(input())
    
A, B = map(int, input().split())
    
# 1. 촌수는 Tree형태 그래프인데, 문제에서 부모(1개만) 저장하는 방식을 택했으니
# -> 1차원 배열에 다가 받아준다. 
# -> 자신의 부모를 모두 0으로 초기화 해놓는다. (1부터 시작하는 node -> 0은 부모가 없다는 것을 표현함.)
# cf) 자식들y는 여러개일 수 있어서  index에 놓고, 각 자식들에 대한 부모는 1명밖이다 -> value로서 1개
p = [0 for _ in range(N+1)]
    
# 2. 관계수를 for문에서 바로 받아, 각 관계 -> 부모배열을 채운다.
for _ in range(int(input())):
    x, y = map(int, input().split())
    # * 3.우리는 1차원 배열에 [부모만!] 저장한다.
    # 1 2 중에 1이 부모니까 index 2에다가 1를 저장한다.
    # cf) 자식들y는 여러개일 수 있어서  index에 놓고, 각 자식들에 대한 부모는 1명밖이다 -> value로서 1개
    p[y] = x
    
# 3. A와 B의 공통 조상을 찾기전에,
# * A의 조상들을 모두 모은다, B의 조상들을 모은다 -> 교집합?
# ** 참고로, A조상을 모을 때는, A자신을 포함해서 A자신 정보, 촌수거리0 부터 시작해서 -> 재귀적으로 (부모, 부모까지거리(+=1)의 정보를 호출해서 담는다.
Aa, Ba =[], [] # Aa: A의 조상a, Ba : B의 조상a
# * A의 조상들(부모, 부모의 부모.. ) 모으는 과정에서, A와의 촌수도 같이 튜플로 저장하기 위해
Ad, Bd = 0, 0
# 1) 자신x<-부모p[x]로 업데이트하여, 부모의 부모도 다음번에 찾아가게함
# 2) 자신<-부모 업데이트할 때, 거리도 +1 업데이트해서, 촌수도 올라가게 함.
# 3) p[x] > 0를 while if조건절에 놓아서, p[x]==0 부모가없는 지점까지 올라간다.
while p[A]>0:
    # 3-1) 제일처음에 들어가면, 나와의거리Ad=0인.. 나 자신을 0촌 조상으로 튜플로 넣어준다. (나, 나와의거리)
    Aa.append( (A, Ad))
    # 3-2) 재귀적으로 내가 부모가 되도록 업데이트해서, 
    # while p[updated A]부모의부모가 있다면 -> (나 updated A=부모, 전보단 늘어난 거리updated Ad +1)
    # 을 조상으로서 재귀적으로 모아준다.
    Ad+=1
    A = p[A] # 내가 내 부모가 된다. for 다음단계를 위한 업데이트
    
# * 부모가 없는 p[A]=0의 root node도 넣어줘야한다... root node가 공통조상이 될 확류은 높다.
# - 현재 p[A]==0상태이며, 첫 0이라서.. 루트노드로 업데이트된 것 일 것이다.. 마지막에 한번만 넣어주자.
Aa.append((A, Ad))
    
# 4. B도 마찬가지다. 
while p[B]>0:
    Ba.append( (B, Bd))
    Bd+=1
    B = p[B] 
Ba.append((B, Bd))
    
    
# print(p)
# * 5.  2개배열을, <2중 포문>으로 1:1매칭 해보면서, 튜플 (조상, 촌수) 중 조상이 같을 때를 찾늗나.
# -> 조상이 같은 순간에서 촌수를 더해버리면 된다.
for i in Aa:
    for j in Ba:
        # 여기는 Aa, Ba 조상들의 1:1매칭 공간
        if i[0] == j[0]:
            print(i[1]+j[1])
            # 등장하면, 제일 빠른 것을 만난 순간 바로 프로그램을 종료하면 된다.
            exit()
else:
    print(-1)

  • 나가는 간선외 들어오는 간선(indegree)까지 있으면 Graph

    • 그래프는 2가지 저장방법이 있음

      • 인접행렬 : 행: 출발점 -> 열: 도착점을 나타내는 N by N행렬

        • 인접행렬도 3가지가 있음.
          • 노방향
          • 방향
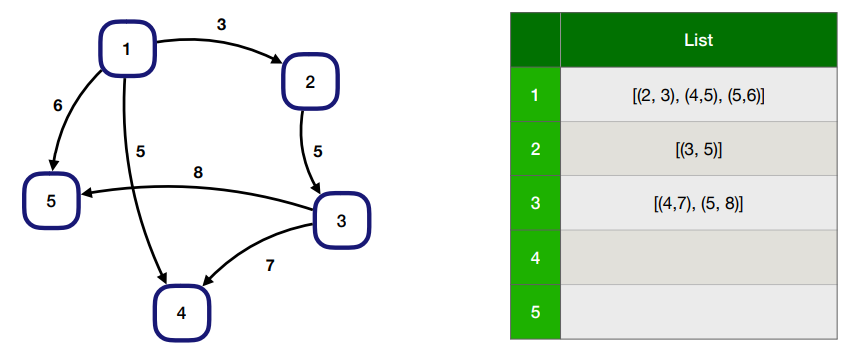
          • 방향+가중치 image-20211027173251556

      • 인접 리스트 : 튜플로 갈수 있는 (가중치, 노드) list를 인접한 list에 저정함.

        • 1의 indegree는? 0 (들어오는게 없다)

        • 1의 outdgree는? 3 (3개가 나간다.)

          • in, outdegree가 중요한 이유는 indegree가 0인 지점이 시작점 일 될 수도, 한붓그리기 는 짝수여야한다. 등의 규칙이 있음

          image-20211027173251556

      • 이렇게 그래프를 저장하면, 최단거리나 가중치를 고려한 최소비용 등을 계산할 수 있게 된다

규칙적용된 tree인 이진트리로 heap/bst

  • 이진트리: Tree구조 자체가 graph만큼 어려워서 규칙을 정했는데
    1. Tree의 rootnode가 1부터가 시작
    2. 자식은 최대2개로 하여->왼쪽자식node == 부모node의 2배가 너넘버링된다.
      • 나node//2 는 부모node
  • heap: NlgN으로 정렬을 유지하면서 데이터 pop/push가 가능하다.
  • bst: python에서는 set, dict의 key를 원소-> hash값 -> hash값들을 bst 구조로 만들어 내부에서 사용되어 중복안되고 bst로 검색해서 빠르다?

그래프, 일반Tree, 점, 격자판 다 탐색하는 DFS와 BFS

  • DFS
    • 전수조사시 사용되하는데, 1->0 마지막 탐색지점에서 빽할 때, 직전 node가 필요한데, 직전node를 stack 선언후 쌓아두는게 아니라, 재귀를 이용해서 stack을 자동 사용한다.
      • 재귀함수=함수=stack메모리에서 관리되어 stack처럼 쓰임
  • BFS
    • 시작좌표(시작점, root node)에서 시작하여
      • level별 = 최단거리별 기록하기 위해 queue(deque)을 사용한다.
        • 목표좌표가 나타나는 최단거리(level)을 구하거나
        • 해당 level이 끝났을 때 최단거리의 수?
      • level별로 좌->우순으로 검색한다.
      • queue에 시작좌표를 넣어놓고
        • 빼고 -> (목표좌푠지확인) -> 자식들 탐색 -> 검사 -> 넣기전 자체처리 -> queue에 넣기 -> (level별 시행시 L+=1)
  • 2개의 사용차이
    1. 찾는 범위가 국한되어서 n번안에 찾아지는 것이 확신을 할 수 있을 경우 -> BFS
    2. 모든 범위를 찾아봐야 하는 경우(매 탐색마다 1->0 바뀌는 끝을 찍어야하는 경우?) -> DFS

앞으로 공부하는 방법

  1. 많이풀기
    1. 삼성은 DFS, BFS 30문제정도
    2. 카카오는 Trie를 포함해서 30문제정도
  2. 암기하기
    1. 이해로는 X 많이 쓰면서 암기하는 과정이 필요하다.
    2. 자기만의 템플릿이 있어야 한다.
  3. 주기적 체크하기
    1. 대회?
    2. 안내서 노션