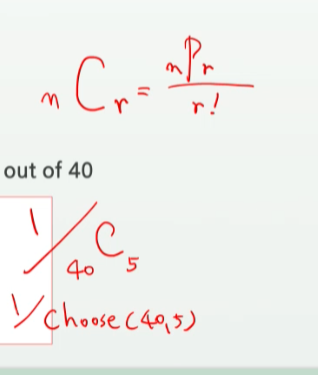데분방02) 확률과 분포 및 기술통계
확률과분포 and Descriptive statistics and graphics
📜 제목으로 보기✏마지막 댓글로
- Probability and distribution
- Chapter 4_Descriptive statistics and 2 graphics
- 4.4 Graphics for grouped data 그룹데이터(1개칼럼 범주별)에 대한 그래프
sample(1:40, 5) #(범위, 갯수)
# 중복허용 여부는 replace=T가 있냐
sample(c("H", "T"), 10)
sample(c("H", "T"), 10, replace=T)
# 각 벡터별로 나올확률을 정해준다.
# 각 원소들 뽑을 확률도 벡터로 직접 지정해줄 수 있다 prob=
# -> 이렇게 확률주고 뽑을 것이면, binomial 분포(이항분포)에서 뽑는 기능도 좋다
sample(c("succ", "fail"), 10, replace=T, prob = c(0.9, 0.1))
# 1/ 40 C 5
1 / choose(40,5)
prod(5:1)
# my) 팩토리얼은 nPr에서 -> r 입력이 아니라 ( n-c+1)을 입력해줘야한다.
prod(5:1) / prod(40:(40-5+1))
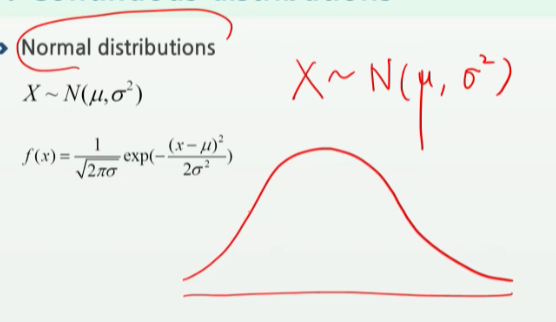
3.5 The built-in distributions in R
-
R에서 제공하는 분포구해주는 함수
-
확률밀도함수: Density or point probability
- 누적분포함수: Cumulated probability, distribution function
- 퀀타일값: Quantiles
- 정규/이항분포 등을 따를 때의 랜덤넘버: Pseudo-random numbers
※ For the normal distribution, these are named
dnorm(확률밀도함수), pnorm(누적 확률함수 분포), qnorm(퀀타일), and rnorm(랜덤넘버) (density,
probability, quantile, and random, respectively).
x <- seq(-4,4,0.1) # 1. seq()으로 예시 x를 뽑았다.
plot(x,dnorm(x),type="l") # 2. plot + x와 y로는 확률밀도함수 dnorm(x)로 그렸다.
title("Normal distribution")
# 예시x대신 from, to를 지정해주는 curve()를 이용한다.
# y값으로 dnorm(x)
curve(dnorm(x), from=-4, to=4)
x <- 0:50 # 1. x를 인덱싱으로 0부터 n까지 정수로만 구성하고
plot(x,dbinom(x,size=50,prob=.33),type="h") # plot + y값으로 d bi nom을 이용했다.
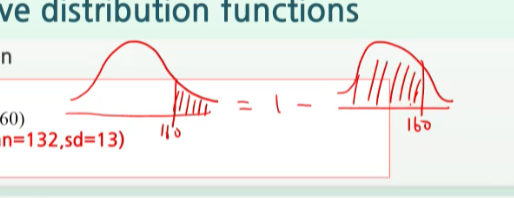
# Q. X가 160보다 클 확률은??
# -> 계산은 [k이하 확률]이 바로 나온다고 생각하자.
# -> 1(전체확률) - (160이하 확률) = 160이상 확률
# my) 정규분포에서 [확률분포 그림상] 확률변수가 k이상/이하 확률 계산은 -> p norm으로 한다.
# 중요!
# my) [확률분포 그림] == [왼쪽 끝부터 k이하까지 누적되는 누적확률분포 p norm]으로 계산한다!
# 분포그림상 문제 -> 누적확률분포상 [왼쪽끝~k이하를 계산해주는 p norm]이용하기
1 - pnorm(160, mean=132, sd=13) # (왼쪽끝부터~k이하에서의 k , 정규분포m, 정규분포sd)

# 20명의 환자에게, A/B 두가지 시험을 각각 함
# -> 16명이 A를 더 좋아함.
# -> A가 더 좋은 treament인지에 대한 충분한 증거가 있는지 확인하기
# how? why?
# **A가 더 좋은 treament다 == 나오는 확률이 반반보다 높을 것이다.로 증명하고 잇넹**
# 1) A or Not A(B) 2가지 경우이며, 확률은 0.5 반반이라고 가정한다. -> 이항분포 따른다.
# 2) 귀무가설H0 -> p = 0.5 확률 반반이라고 정한다.. why?
# 3) p-value 계산 -> 귀무가설H0(p=0.5)하에 [현재상황인 X=16명]이상일 확률을 구한다.
# -> 1 - P(X <=15명이하)
# --> my) 더 좋은 치료는 아니다 == 확률 반반이다 상태로 -> 현상황에서 꼭다리를 구함
# 4) [귀무가설하 꼭다리 = p-value]가 0.05보다 작다? -> 귀무가설 반반은 틀린 것.. 0.5보다 클 것이다. -> 더 좋은 치료다
1 - pbinom(15, size=20, prob=.5) # 계산결과가 p-value다
중간 내 정리(누적확률분포 함수)
-
정규든 이항이든 누적확률분포는 현재 확률변수 X가 가진 분포에 대해
왼쪽끝 ~ k이하까지의 면적 계산해서 확률을 응답해준다. -
p-value 계산은 H0에서
k이상일 확률(꼭다리)를 물어볼 것이다. ->- 1 -
(왼쪽끝~k이하) by 누적확률분포 함수pnorm or p bi nom
- 1 -
-
case와 확률이 둘다 0.5인 treatment에서 -> 어떤 치료가 더 좋다?(반반 아니다)를 증명하려면?
-
P=0.5가 아니다를 증명해야하는데 -
(1)뒤집어질 귀무가설
P=0.5을 귀무가설로 잡고 -> (2)해당하는 분포 함수를 만들고이항분포를 만들고 -> (3)분포 함수내에서 p-value계산을 위해, H0의 x값 k를 구한 뒤,1- (왼쪽끝~)k이하확률은 누적확률분포 함수에 k를 넣어서-> p-value(k이상 확률)을 구한다k이상의 꼭다리 계산후 -> 꼭다리 계산결과 자체가 = p-value이며p-value가 0.05가 낫다를 증명해야한다.
-
p norm이나 p bi nom등의누적확률분포 함수로 -> 정규분포와 이항분포의p-value를 계산할 수 있다.
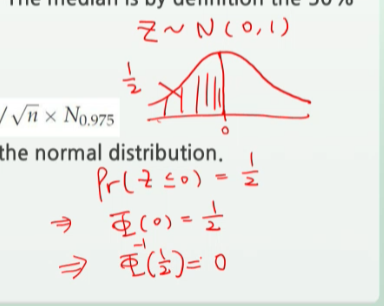
- 누적확률분포 함수의 역함수라는 것을 이용하면, 퀀타일로
신뢰구간을 구할 수 있다.-
95% CI(신뢰구간)for m이다?- 표준 정규분포 양측 총 5% 내에 들 확률?
- 표준 정규분포 각 측의 2.5%내에 들 확률?
- 표준 정규분포 (왼쪽끝~ N 0.025) = 0.025가 되는 값?
- 표준 정규분포 (반대편에서 ~N 0.975) = 0.025가 되는 값?

-
xbar <- 83
sigma <- 12
n <- 5
# S/루트(n) = 표준오차
sem <- sigma/sqrt(n)
sem
my) qnorm : 신뢰구간% / 100의 값에 대해 , 이미 정해진 Z분포에서 한쪽끝 확률을 0.5중앙에서부터 방향대로 주기
- qnorm(0.025)
- 0.025 -> 한쪽끝 2.5% -> 양쪽 5%의 신뢰구간에 대해
- 0.5부터 면적확률을 계산해주는 데,
- 왼쪽으로 가면 음수 ex> qnorm(0.025) = N0.025 <-- N0.5 : 확률이 음수로
- 오른쪽으로 가면 양수로 반환해주니 ex> N0.5 --> N0.975 : 확률이 양수로
- xbar에서 편하게 더하기만 하면 된다.
- xbar± Z(0.975) * s/sqrt(n)
- xbar
- Z(0.975)s/sqrt(n) = **`xbar +qnorm(0.025) s/sqrt(n)`** - xbar + Z(0.975) s/sqrt(n) = = **`xbar +qnorm(0.975) s/sqrt(n)`**
- xbar
- xbar± Z(0.975) * s/sqrt(n)
qnorm(0.025)
qnorm(0.5)
xbar + (sem * qnorm(0.025))
xbar + Z(0.975) * s/sqrt(n) = = xbar +qnorm(0.975) * s/sqrt(n)
xbar + (sem * qnorm(0.975))
rnorm(10)
rnorm(10)
rnorm(10, mean=7, sd=5)
rbinom(10, size=120, prob =.5)
rt(10)
x <- rnorm(50) # 표준정규분포 랜덤 50개
mean(x) # 평균
sd(x) #표준편차
var(x) # 분산
median(x) # 중앙값
quantile(x) # 4분위 값 -> 최소+최대, 1,3분위수, 중앙값 다 등장한다
pvec <- seq(0, 1, 0.1)
pvec
quantile(x, pvec)
library("ISwR")
data(juul)
head(juul, 3)
attach(juul)
mean(igf1)
mean(igf1, na.rm=T)
igf1
#sum(igf1, na.rm=T)
sum(!is.na(igf1)) # NA를 제외한 갯수
summary(igf1) # NA의 갯수를 한번에
summary(juul)
detach(juul)
juul$sex <- factor(juul$sex, labels = c("M", "F"))
juul$menarche <- factor(juul$menarche, labels = c("No", "Yes"))
juul$tanner <- factor(juul$tanner, labels = c("I","II","III","IV","V"))
attach(juul)
summary(juul)
# sex=factor(sex,labels=c("M","F")),
# menarche=factor(menarche,labels=c("No","Yes")),
# tanner=factor(tanner,labels=c("I","II","III","IV","V")))
x = rnorm(50)
x
hist(x)
mid.age <- c(2.5,7.5,13,16.5,17.5,19,22.5,44.5,70.5)
acc.count <- c(28,46,58,20,31,64,149,316,103)
age.acc <- rep(mid.age,acc.count)
brk <- c(0,5,10,16,17,18,20,25,60,80)
hist(age.acc, breaks=brk)
n <- length(x)
n
(1:n)/n
# y는 총갯수에 대해 1,2,3,4... n 까지 나열하는데 값을 /50 -> 0부터 1까지를 50등분?
# x정규분포 50개의 값과 무관하게,
# y는 0부터 1까지 점점 커지는 n등분
plot( sort(x), (1:n)/n)
# y는 0부터 1까지 점점 커지는 n등분
# type="s"를 통해, 산점도를 계단식의 선으로 표현
plot( sort(x), (1:n)/n,
type="s"
)
# y는 0부터 1까지 점점 커지는 n등분 -> n개의 x에 대해, 자신의 위치?
# type="s"를 통해, 산점도를 계단식의 선으로 표현
plot( sort(x), (1:n)/n,
type="s",
ylim=c(0,1)
)
library("stats")
ecdf(x)
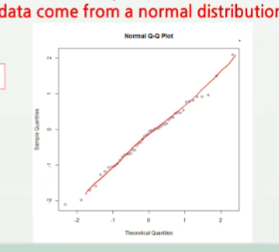
qqnorm(x)
library(ISwR)
par(mfrow=c(1,2))
boxplot(IgM)
boxplot(log(IgM)) #
# 복구
par(mfrow=c(1,1))
attach(red.cell.folate)
head(red.cell.folate, 3)
# folate ventilation
# 1 243 N2O+O2,24h
# 2 251 N2O+O2,24h
# 3 275 N2O+O2,24h
# 그룹별 folate의 평균
tapply(folate,ventilation,mean)
tapply(folate,ventilation,sd)
tapply(folate,ventilation,length)
xbar <- tapply(folate, ventilation, mean)
s <- tapply(folate, ventilation, sd)
n <- tapply(folate, ventilation, length)
cbind(mean=xbar, std.dev=s, n=n)
tapply(igf1, tanner, mean)
tapply(igf1, tanner, mean, na.rm=T)
aggregate( juul[c("age","igf1")], list(sex=juul$sex), mean, na.rm=T)
by( juul, juul["sex"], summary)
attach(energy)
expend.lean <- expend[stature=="lean"] # 범주종류별로 개별칼럼 만들기 by 인덱싱
expend.obese <- expend[stature=="obese"] # 범주종류별로 개별칼럼 만들기
# 범주종류별 개별칼럼을 개별로 그리기
par(mfrow=c(2,1))
hist(expend.lean,breaks=10, xlim=c(5,13),ylim=c(0,4),col="white")
hist(expend.obese,breaks=10, xlim=c(5,13),ylim=c(0,4),col="grey")
par(mfrow=c(1,1))
# boxplot(데이터 ~ 범주종류를 가진 범주칼럼)
boxplot(expend ~ stature)
# boxplot(범주1칼럼, 범주2칼럼)
boxplot(expend.lean, expend.obese)
opar <- par(mfrow=c(2,2), mex=0.8, mar=c(3,3,2,1)+.1)
stripchart(expend ~ stature) # 1x1 :
stripchart(expend ~ stature, method="stack") # 1x2 stack
stripchart(expend ~ stature, method="jitter") # 2x1 겹치는 것을 피하기 위해 약간 흔들어서
stripchart(expend ~ stature, method="jitter", jitter=.03) # 2x2 덜 세게 흔들기
par(opar)
caff.marital <- matrix(c(652,1537,598,242,36,46,38,21,218,327,106,67), nrow=3,byrow=T)
caff.marital
colnames(caff.marital) <- c("0","1-150","151-300",">300")
rownames(caff.marital) <- c("Married","Prev.married","Single")
caff.marital
# 여기선 안보이는 듯 -> matrix -> table -> dataframe으로 만들면 보이게 된다.
names(dimnames(caff.marital)) <- c("marital","consumption")
caff.marital

as.data.frame(as.table(caff.marital))
# 실제 작업을 한다면, 첫번째 case는 652만큼 더 읽어라? 로 작업? by rep
head(juul, 2)
table(sex)
table( sex, menarche)
xtabs( ~ sex + menarche, data=juul)
tanner.sex <- table( tanner, sex )
tanner.sex
margin.table( tanner.sex , 1) # 가로1 -> 행별로 빈도수 총합 보기 (row그룹의 범주별 빈도만 보기)
margin.table( tanner.sex , 2) # 세로2 -> col그룹의 범주별 빈도만 보기
prop.table( tanner.sex, 1)
prop.table( tanner.sex, 2)
caff.marital # matrix
total.caff <- margin.table( caff.marital, 2) # 칼럼종류렬 빈도만 보기
total.caff
barplot( total.caff, col="white")
caff.marital
t(caff.marital)
par(mfrow = c(2,2))
barplot(caff.marital, col="white") # matrix형태의 barplot은 자동 stack
barplot(t(caff.marital), col="white") # t()로 뒤집어서 반대가 stack으로 들어가고 stack은 x축으로 표기됨
barplot(t(caff.marital), col="white", beside = T) # stack을 푸는 옵션
barplot(prop.table(t(caff.marital),2) , col="white", beside = T) # 빈도수 -> 비율로 바꾸는 옵션
# prop.table( ,2)로 주어서, 세로칼럼별 = stack이 풀려져있는 덩어리들별로.. 비율구해주기
par(mfrow=c(1,1))
barplot(prop.table(t(caff.marital),2) , col="white", beside = T,
legend.text = colnames(caff.marital)
)
barplot(prop.table(t(caff.marital),2) , beside = T,
legend.text = colnames(caff.marital),
col = c("white", "grey80", "grey50", "black")
)
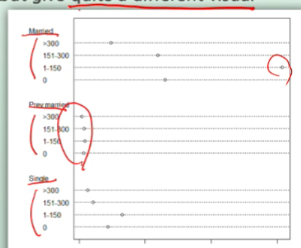
dotchart(t(caff.marital), lcolor="black")
# row가 왼쪽에 먼저
# col은 왼쪽에 depth넣고
opar <- par(mfrow=c(2,2),mex=0.8,mar=c(1,1,2,1))
slices <- c("white","grey80","grey50","black") # col=에 넣을 컬러들 미리 빼놓기
pie(caff.marital["Married",], main="Married", col=slices)
pie(caff.marital["Prev.married",], main="Previously married", col=slices)
pie(caff.marital["Single",], main="Single", col=slices)
par(opar)