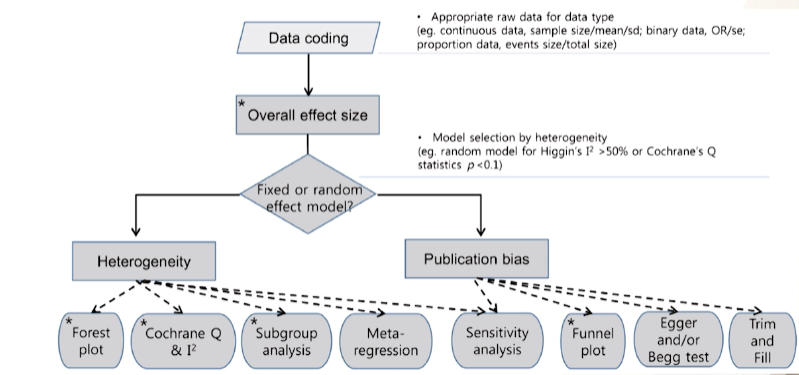
의연방12) 메타분석2(메타분석 4단계)
Meta Analysis의 과정
📜 제목으로 보기✏마지막 댓글로
- 학습목표
- 목차
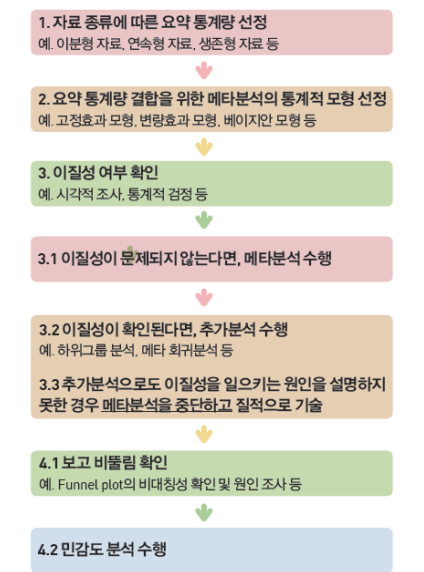
- 메타분석의 절차
- 01 요약통계량선정
- 02 통계모형 선정
- 03 이질성 확인
- 04 Publication bias 확인
- Summary for meta analysisprocess
- 연습문제
- 정리하기
주요용어
-
메타분석 : 체계적 문헌 고찰 수행과정에서 2개 이상의 개별 연구의 요약 통계량을 합성함으로써 해당 중재법의 통합된 가중평균 요약 통계량을 정량적으로 산출하여 임상적 효과성을 평가하기 위해 사용되는 통계적 기법
-
고정효과모형 : 각 연구들에 있어 중재효과의 참값은 단 하나만 존재(common true treatment effect)한다는 전제 하에 관찰된 치료효과 값들의 차이는 표본추출의 오차 때문이라는 가정에서 출발하는 모형
-
변량효과모형 : 각 연구들에 있어 중재효과의 참값은 단 하나만 존재하는 것이 아니라 각 연구들에 있어 중재법의 효과는 어떤 중재효과의 평균 참값(true average treatment effect)을 중심으로 정규분포를 따른다고 가정하는 모형
-
이질성(Heterogeneity) : 메타분석에 포함된 개별 연구들의 결과간 변동(variation)이 표본추출 오차 이상으로 관찰되어 우연으로 설명할 수 없는 것
-
출판 비뚤림 (publication bias) : 연구결과의 통계적 유의성과 출판 가능성간의 관련성이 있을 때 나타나는 비뚤림이며, 통계적으로 유의한 긍정적인 연구결과인 경우 더욱 더 잘 출판될 가능성이 있기 때문에 발생하는 비뚤림
01 요약통계량선정
- 결과(outcome) 타입의 종류는 총
3가지이다.- 이분형변수: event가 있었다/없었다 평가되는 경우
- 연속형 자료
- 생존형 자료
이분형 자료(Binary outcome)
- summary measrue로서 3가지 중 1개를 선택해서 메타분석의 main result로 제시한다.
- Risk Ratio/Relative Risk (RR)
- 두 군간 사건이 발생 비율에 대한 비
-
Odds Ratio (OR) : 가장 많이함. 코호트나 RCT세팅일 땐,
RR을 제시하는 것이 summary measure로서는 더 적절하다. OR는 대안일 뿐이다.- 두 군간의 사건의 승산에 대한 비
- Risk Difference (RD)
- 두 군간 사건 발생 비율의 차이
- Risk Ratio/Relative Risk (RR)
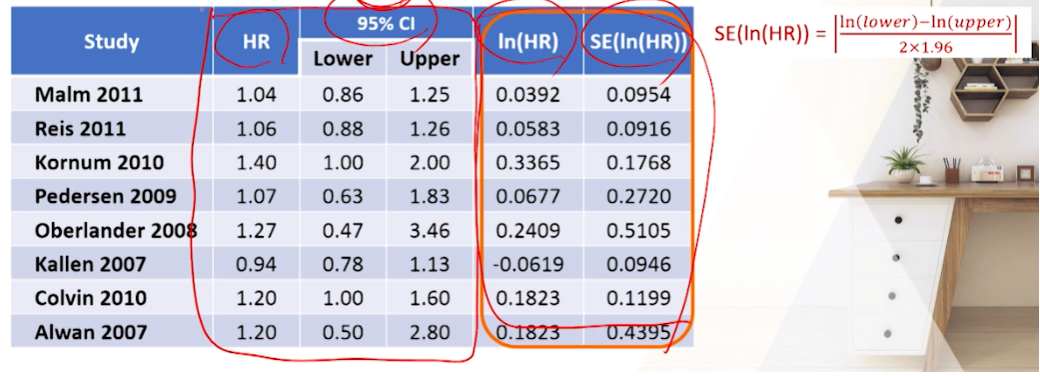
- 계산하기 위해서는 각 군에 배정된 환자 수에 대해 사건이 일어난 수를 이용한다.
- 표에서 각 row별
3가지 데이터 중 2가지만 추출하면 메타분석이 가능하다.
- 표에서 각 row별
- 2015 논문 예시
- 뇌졸중 환자에 대해 Cilostazol이 Control(위약, 아스피린 등)에 비해 뇌졸중 발생 event가 줄어들어 예방하는지를
RR로 summary method로 제시함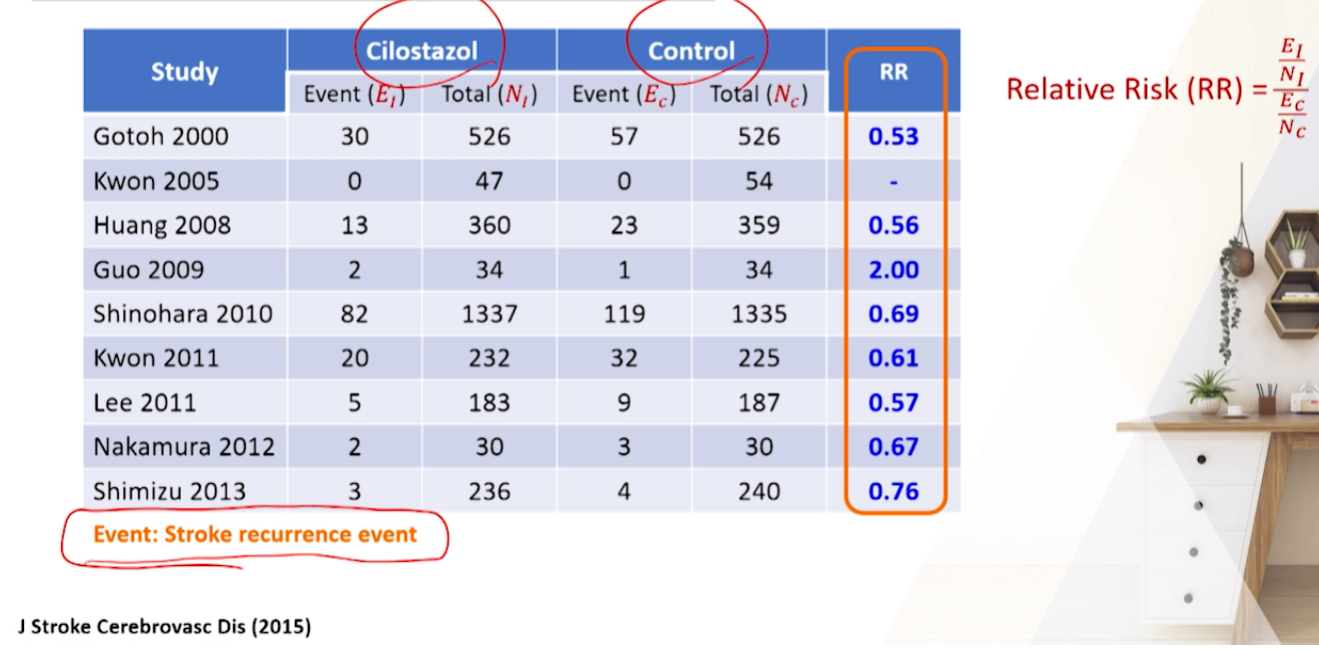
- 각 군의 환자 수 -> 대부분 RCT연구이기 때문에 치료군/대조군 수가 비슷함.
- 각 군의 event수를 확인해봤더니 2번째 논문에서는 Event(뇌졸중 발생)수가 0다
- 가장 안좋은 예임. 두 군에서 1건도 발생안하면 -> RR 추정이 안되어 -> 메타분석 논문에서 빠지게 됨.
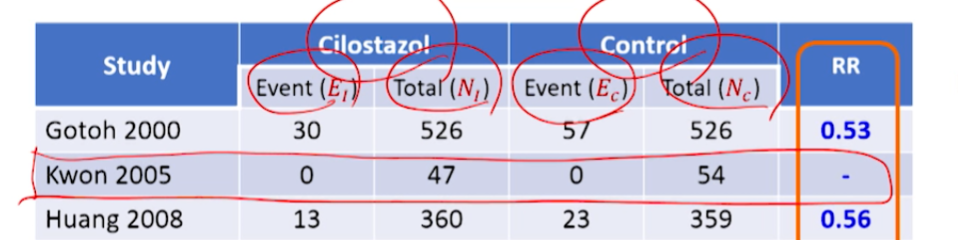
- 가장 안좋은 예임. 두 군에서 1건도 발생안하면 -> RR 추정이 안되어 -> 메타분석 논문에서 빠지게 됨.
- RR 전까지
각 군의 N수 + event 수를 raw data라고 한다.
- 뇌졸중 환자에 대해 Cilostazol이 Control(위약, 아스피린 등)에 비해 뇌졸중 발생 event가 줄어들어 예방하는지를
연속형 자료(Continuous outcome)
- 가장 대표적인 연속형 자료의 summary measure는
평균이다.- 이분형 변수는 각 군의 N수 + event수 2가지만 필요했지만
- 연속형 변수는 각군의 N수 +
M(평균) + 표준편차3개가 필요하다.- 선택적으로서 baseline대비 Change를 볼 것인지, 최종값(Final)을 볼 것인지 선택한다.

- 선택적으로서 baseline대비 Change를 볼 것인지, 최종값(Final)을 볼 것인지 선택한다.
-
평균의 차이를 보더라도, 각 논문마다 측정 단위가 다를 수 있다. 1.Mean Difference (MD)
- 동일한 측정도구로 측정되었을 때- Standardized Mean Difference(SMD)
- 동일한 결과를 다양한 측정도구로 측정하였을 때
- Standardized Mean Difference(SMD)
-
BMJ 논문 예시: MD를 썼다. +면 체중 증가 / -면 체중 감소를 의미
- MD를 썼다 = 각 논문마다 측정단위가 동일했다.
- raw data에는 N + 평균 + SD 3가지가 들어간다.
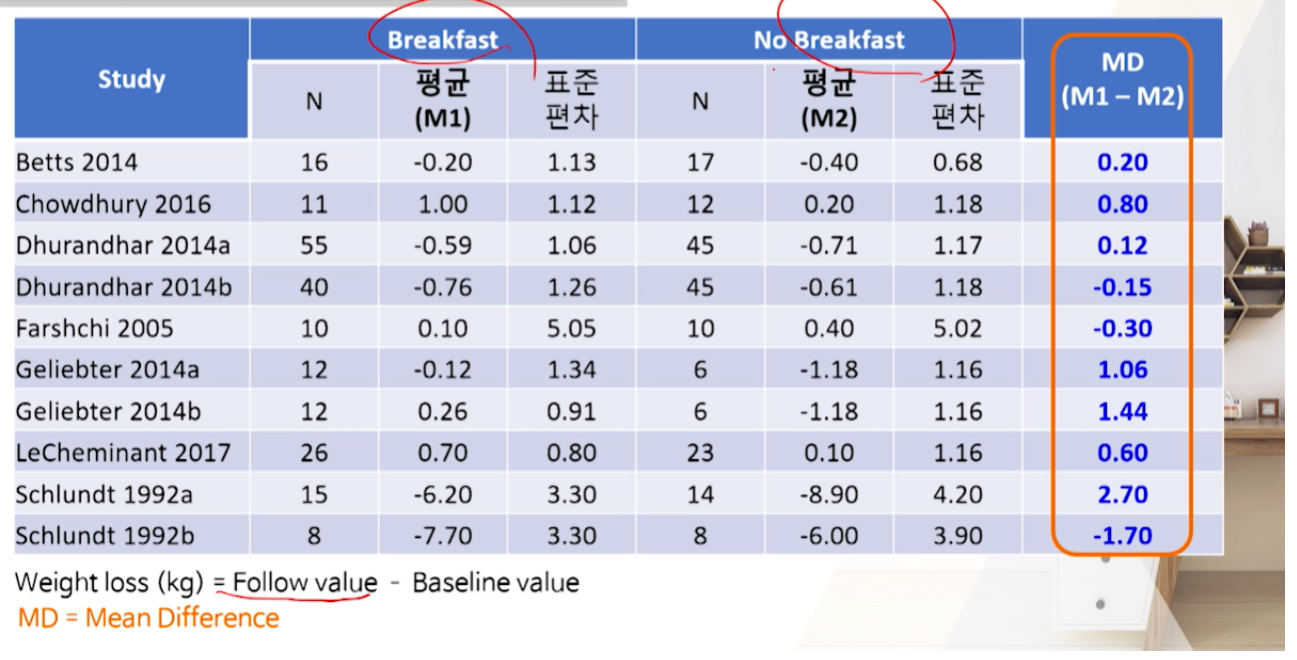
-
논문 마다 baseline + final 값을 제시할지 / change값(follow - baseline)을 제시할 수도 있다.
- 만약, baseline + final 값을 제시한다면 -> change값으로 환산하는 노력이 필요하다
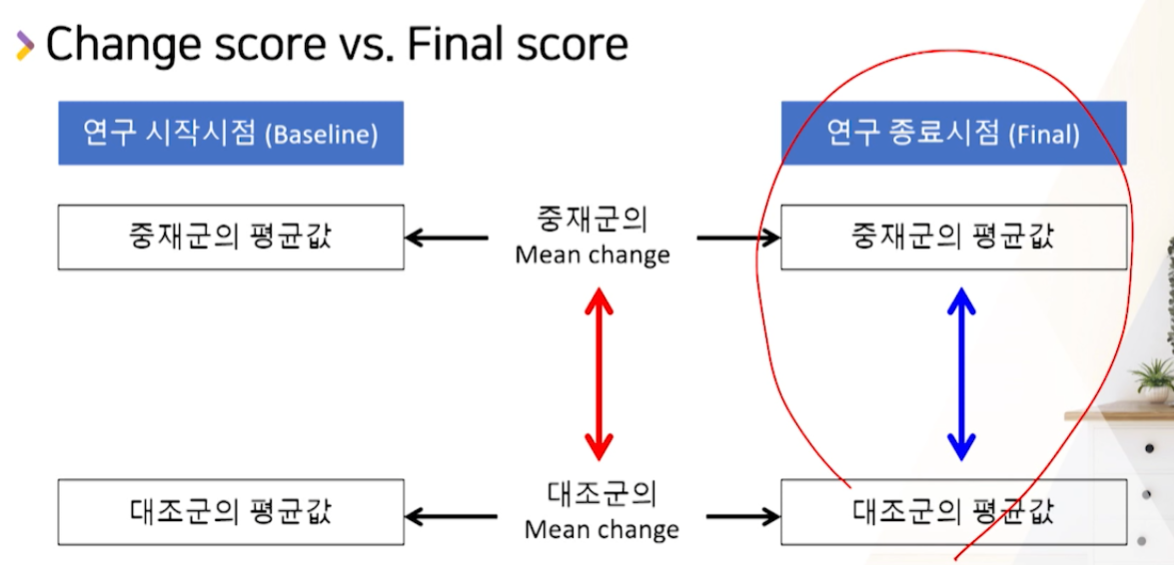
- 만약, baseline + final 값을 제시한다면 -> change값으로 환산하는 노력이 필요하다
-
논문마다 N + Mean + SD 가 아니라 Mean대신 중위수 or 4분위수 등을 줬다면, raw data로서 못쓸까?
- Mean + SD로 변화하는 도구(R)가 있다.
-
결과적으로 outcome이 연속형 변수의 논문인 경우,
N + 평균 + 표준편차를 추출해야 raw data로 쓸 수 있다는 것을 기억하자
02 통계모형 선정
- 데이터 추출된 상태(summary measure결정 + raw data확보)라고 가정하고 결합해서 메타분석시 사용할 통계모형을 선정해야한다.
- 결과적으로 RR이나 MD가 논문마다 나올 것인데, 이것들을 결합해서
총합된 요약통계량을 제시해야한다.
- 결과적으로 RR이나 MD가 논문마다 나올 것인데, 이것들을 결합해서
Combining study results
-
각 연구자료 내 요약 통계량 선정 후 이를 어떻게 취합하는가?
- 마치 한 개의 연구인 것처럼 취합 – 치료군은 치료군대로, 대조군은 대조군대로 합산?
-
흔하게 하는 실수로, 논문별로 칼럼별로
event수를 단순하게 다 더해서 통합된 RR을 구하는 것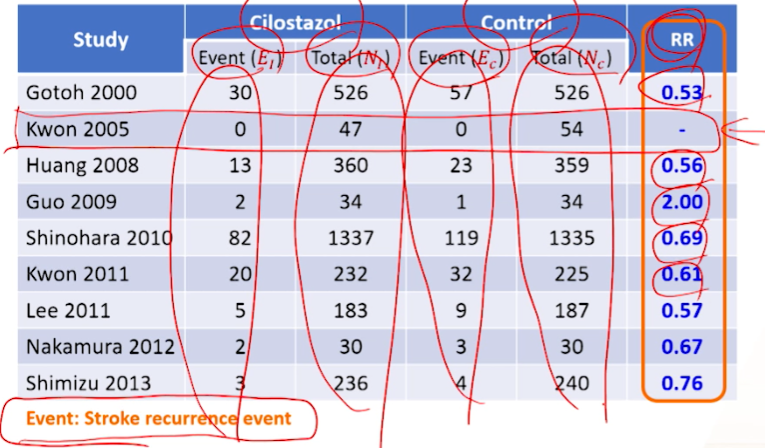
-
흔하게 하는 실수로, 논문별로 칼럼별로
- 무작위 배정 위반으로, 잘못된 결과 도출됨
- 마치 한 개의 연구인 것처럼 취합 – 치료군은 치료군대로, 대조군은 대조군대로 합산?
-
단순 평균?
- 모든 연구자료가 동등한 비중인 것처럼 간주하는 것
MD를 평균내는 행위 -> 모든 스터디들이 N수가 다름(2000명 vs 30명 -> 동일한 비중을 가지게 만들어버림. 2000명 논문저자는 억울하다. 신뢰성.)
-
가중치가 부여된 평균 (weighted average)- 더 많은 정보를 주는 개별연구에 보다 많은 가중치 부여
- 가중치 주는 기준
-
더 많은 참여자: 자료추출시 n수 추출은 WEIGHT를 더 주기 위함이다. -
많은 사건 수:n수가 비슷할 경우 capture한 사건 수가 비슷할 때 - 보다 좁은 신뢰구간: 경우에 따라 quality에 따라 weight
-
- 효과 추정 및 변이(variation) 를 사용하여 계산
2가지 통계모형
고정효과모형 (Fixed effect model)
-
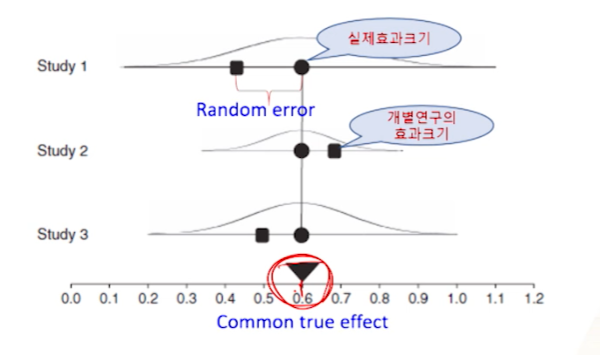
실제 효과는 고정되어있다고 보고, study마다 다른 결과를 나타내는 이유는sampling variation(모집단이 아닌 표본추출로 인한 변동)에 의한 것이라고 보는 모형- 대규모 연구일 경우, sampling이 많아 모집단에 가까운 연구결과를 내고 적으면 그 반대
-
sampling variation이 기반으로 하는
N수기반으로 weight를 주는 모형- small study -> variation 크다.
- large study -> variation 작다.
- weight를 variable의 역수를 주어 반대로 반영한다.
-
고정효과 모형에서의 가중치는 연구 내 변이(within-study variation)만을 고려
- 고정효과 모형에서의 가중치(weight) = 1/ (
연구 내 변이)
-
역-분산(Inverse Variance) 추정법: 결국 표본수n이 클수록 많은 가중치를 반영한다는 뜻.
-
작은 표준오차를 가지는 큰 규모의 연구일수록 가중치를 많이 받음 -
sample size is key (n ↑ = precision ↑ = SE ↓)
- 표준오차 = 표준편차 / 루트(n) -> n수가 커질수록 표준오차는 작아진다.
- 예시: bmj논문
-
n수가 제일 큰 3번째 연구 -> SE(표준오차)가 제일 작다 -> 역수의 제곱을 취했더니 제일 크다 -> weight 제일 크다.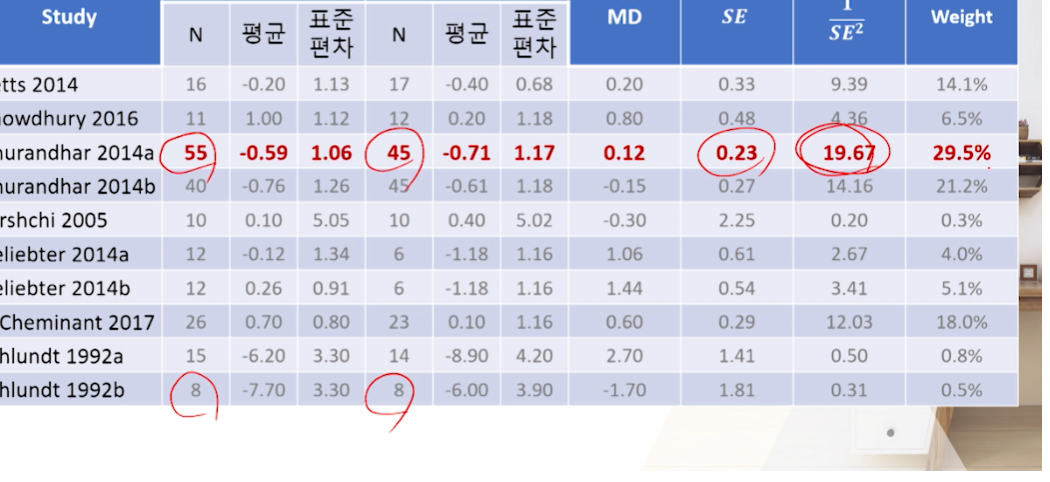
-
-
-
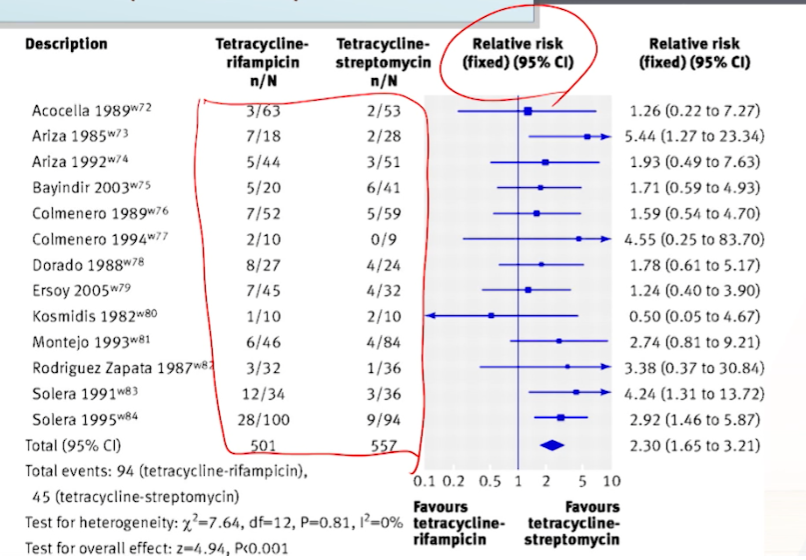
멘텔-헨젤(Mantel-Haenszel) 추정법: binary outcome중에 n수도 있지만, +
event수가 많이 capture된 연구일 수록 weight를 많이 주겠다.- OR, RR, Rate Ratio와 같은 2×2 표를 만들 수 있는 자료에서 사용
- 사건 발생률이 낮거나 연구의 규모가 작지만 메타분석에 포함되는 연구의 수가 많을 때 효과적인 방법
-
OR 또는 RR의 분산(2x2 table에서 n수로 역수를 취해서 분산을 구함 -> n수 뿐만 아니라 event수가 반영됨)의 역수를 개별 연구의 가중치로 사용 - 예시: 뇌졸중 환자 논문
-
RR을 summary measure로 쓰기로 약속한 상태로, RR의 분산은 2x2 table에서 역수를 취해서 분산을 구하므로N수도 중요하지만, event수도 중요하다- 5번째 연구가 50%를 차지하게 된다.
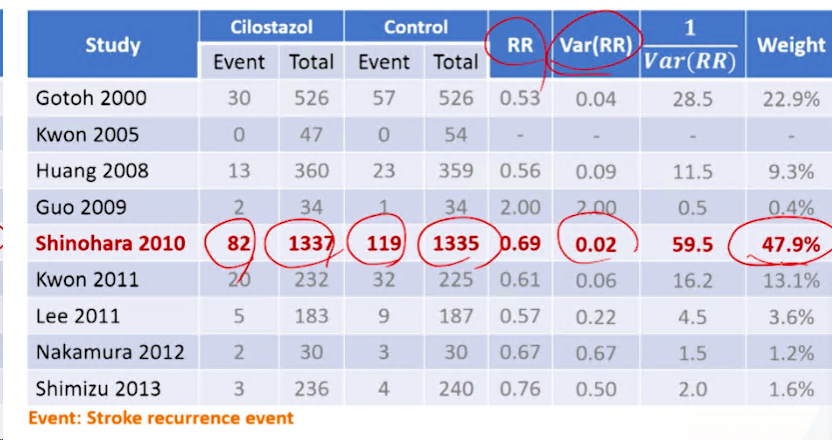
- 5번째 연구가 50%를 차지하게 된다.
-
- 고정효과 모형에서의 가중치(weight) = 1/ (
변량효과모형(Random effect model)
- 각 연구들은 어떤 평균적인 처리효과(average treatment effect)를 중심으로 퍼져있는 모집단 내 연구들로부터 무작위로 추출된 연구들이라고 가정
-
따라서 처리효과들간에 variation이 관찰되는 이유는 표본추출 변동(within-study variation)과 연구들 간의 변동(between-study variation)이 함께 나타났기 때문으로 간주
-
고정효과모형의 경우처럼, n수나 event수 기반으로 weight를 부여했었던 것은, 결과적으로 동질화된 연구들로 세팅이 됬을 때 가능한 경우다
- 모집단이 유사하게 세팅된 상태로, 안정적인 상황이다.
-
동일한 모집단에 대한 동일 연구가 아니라,
비슷한 연구들을 넣다보니- study간/study내에서 variation도 존재해버린다.
- study간: 각각의 스터디들(●)이 실제공통효과 (▼)와는 다르게 개별적으로 존재하는 상황에서
- 고정효과모델은 각 스터디들 효과(●) = 실제공통효과(▼)의 공통효과 중심이었음.
- study내: sampling variation -> 표본추출변동 = within-study variation
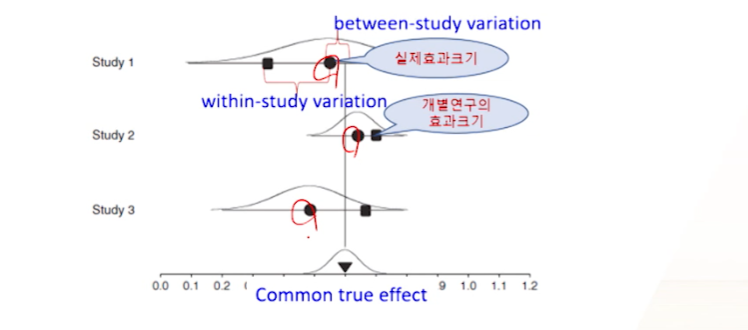
- study간: 각각의 스터디들(●)이 실제공통효과 (▼)와는 다르게 개별적으로 존재하는 상황에서
- n수 event수 뿐만 아니라
스터디간 변동(스터디마다 세팅이 다름)도 반영해서 weight를 줘야한다.
- study간/study내에서 variation도 존재해버린다.
변량효과모형의 가중치 추정방법
-
변량효과 모형에서의 가중치(weight) = 1/(연구 내 변이 +
연구간 변이)- 연구내 변이: 고정효과모델의 변동 = 표본추출 변동 = n수+event수 반영
- 연구간 변이: 비슷한 연구들 = 모집단이 조금씩 다름 = 세팅이 다른 연구들간의 변동도 반영
-
Methods to estimate the between study variance
-
DerSimonian-Laird estimator(default method in many statistical software)- 가장 많이 사용. 메타분석 전용 툴인 Revman에서는 이 방법만 제시한다.
- Paule-Mandel estimator
-
Restricted maximum-likelihood estimator
- 최근에는 advanced한 방법인 2,3번째를 추천하는 경향이 보인다.
- R에서 제공한다.
- Maximum-likelihood estimator
- Hunter-Schmidt estimator
- Sidik-Jonkman estimator
- Hedges estimator
- Empirical Bayes estimator
-
-
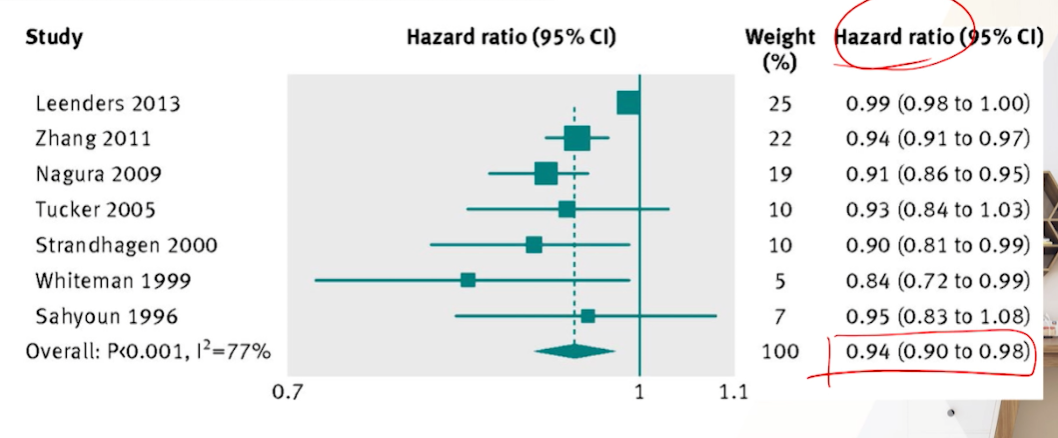
예시: 왜 변량효과모형을 사용할까?
- 임신중독증 환자들에 이뇨제의 효과 메타분석
- 스터디가 오밀조밀 모여있어야하는데, 퍼져있다.
- population이나 이뇨제 세팅이 달라서로 추정
-
스터디 간의 varation을 반영하지 않는Fixed-effectes모형의 경우 효과가 있는 것 처럼 보인다.-
Odds Ratio가 1을 포함하지 않아서, 통계적으로 유의하다로 결론
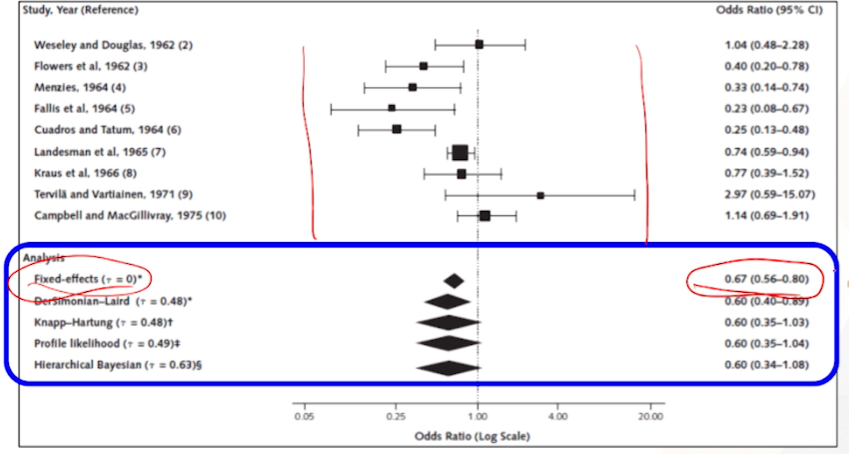
-
Odds Ratio가 1을 포함하지 않아서, 통계적으로 유의하다로 결론
- 문제는 스터디가 너무 다양해서 바로 결론을 내릴 수가 없다. 그래서
DerSimonian-Laird의 방법(by Revman)을 썼는데도 통계적으로 유의하다는 결론이 나왔다. - 그럼에도 불구하고, 더 advanced된 방법인 방법들by R)을 썼더니, OR이 1을 포함하여 통계적 유의성이 없다는 결론이 나왔다.
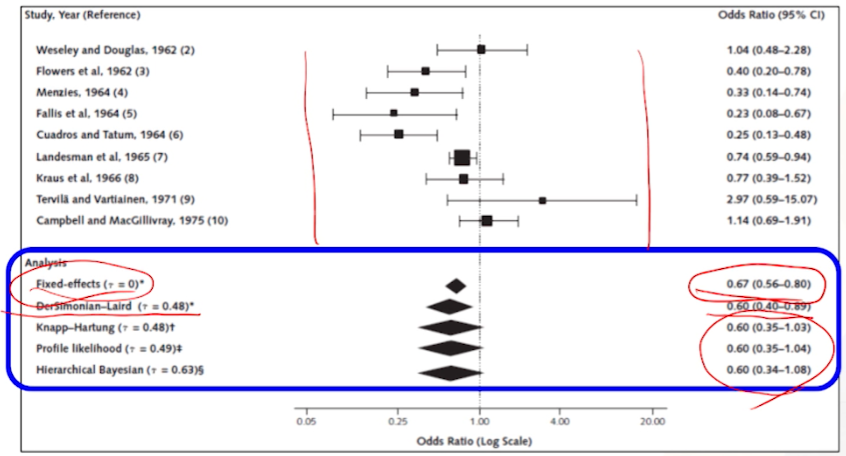
- 더시모니안-레이어드 method방법으로 썼다면, advance로 한번 더 하라고 권고를 하는 상황이다.
- 임신중독증 환자들에 이뇨제의 효과 메타분석
-
우리는 메타분석 초보이다 -> 스터디가 퍼져있으면, Fixed-effects말고 Random-effect모형(varied 모형?)을 쓰는 것만 생각하자.
Software for Meta analysis
-
Review Manager 5.4 (
RevMan 5.4)- https://training.cochrane.org/online-learning/coresoftware-cochrane-reviews/revman
- 학술적 사용은 무료, 상업적 사용은 유료
- 코크만(체계적 문헌고찰을 전문적으로 하는 큰 집단)에서 무료로 제공함
-
Comprehensive Meta-Analysis (
CMA) Version 3.0 ($)- http://www.meta-analysis.com/
- 유료 프로그램
-
Statistical software
- STATA,
R (‘meta’, ‘metafor’ package)
- STATA,
Forest plot (숲 그림)
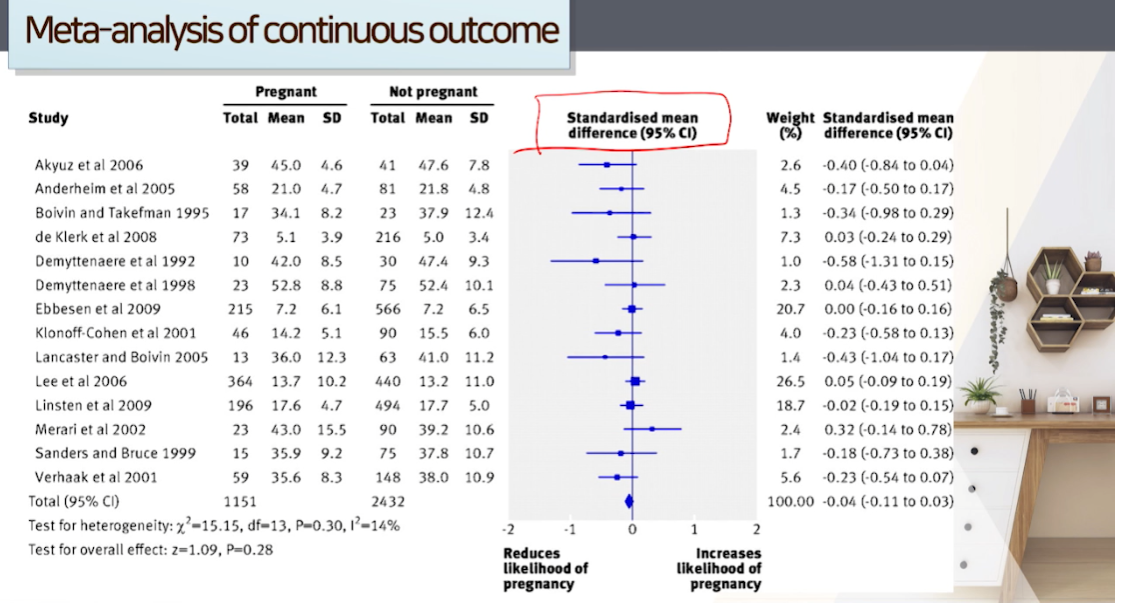
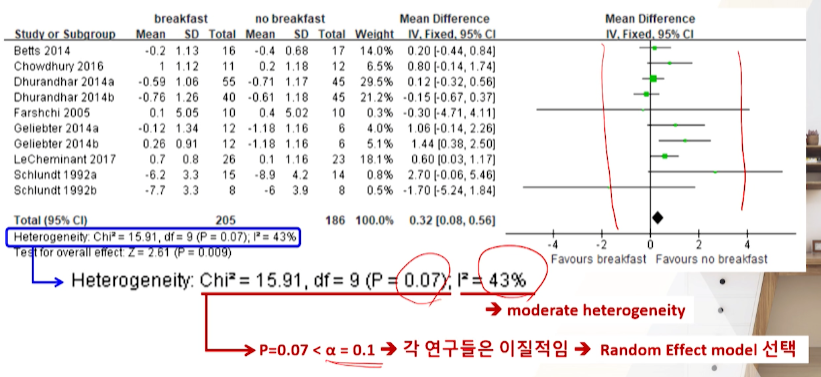
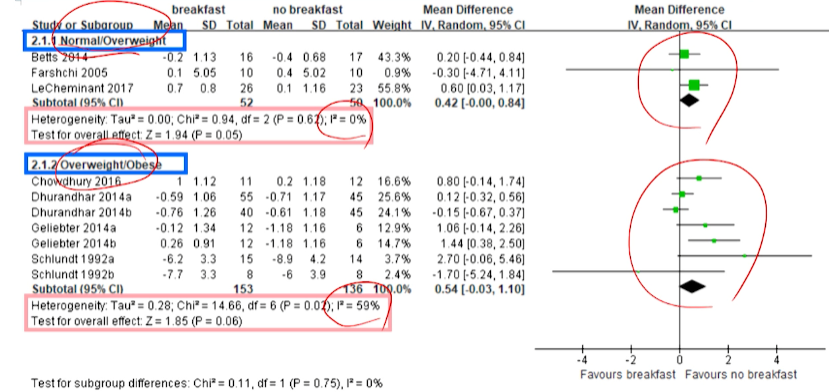
연속형 outcome 예시(weight loss)
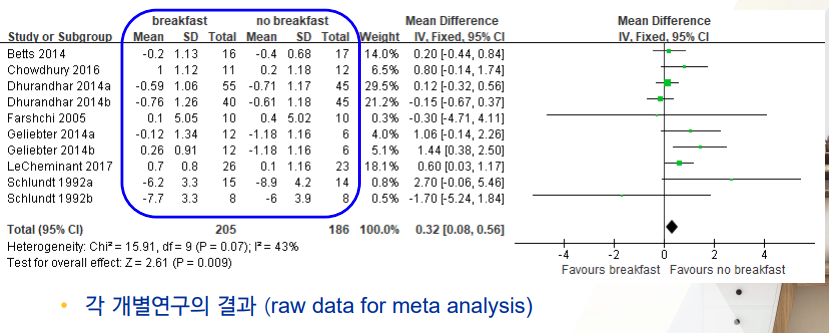
- 메타분석의 기본적인 result다.
-
구성요소
- 개별적 연구 목록들
- raw data 입력값들
- weight
- 그림을 보면 IV(역분산 방법), Fixed(고정효과모형)을 선택한 것으로 보이니 N수 + event수 기반으로 weight가 결정됬을 것이다.
- 그림상 초록색 box의 size를 결정하
- Mean Difference
- raw data를 입력하면 역시 자동으로 계산되는 값
- 척도
- 그림의 아래 부분에서 확인한다. 어느 방향으로 가면 효과가 좋은 것인지 생각하고 본다.
-
total Mean diffrence
- 이 예시에서나오는 0.32의 weighted Mean Difference를 얻기 위해 메타분석을 한 것이다.
-
OR가 다르게 유의한지 안하지 보려면 1이 아닌
0을 포함하는지를 보면 된다.- totla MD가 0을 포함하고 있지 않기 때문에 유의한 결과를 냈다.
- 그 밑에 나타내는 P-value값을 봐도 된다.
- 그림상으로는 큰 다이아몬드가 나타내고 있다.
-
MD가
+방향에 있다 ->우측(아침식사X 군)이outcome(weight loss)에 효과가 더 좋다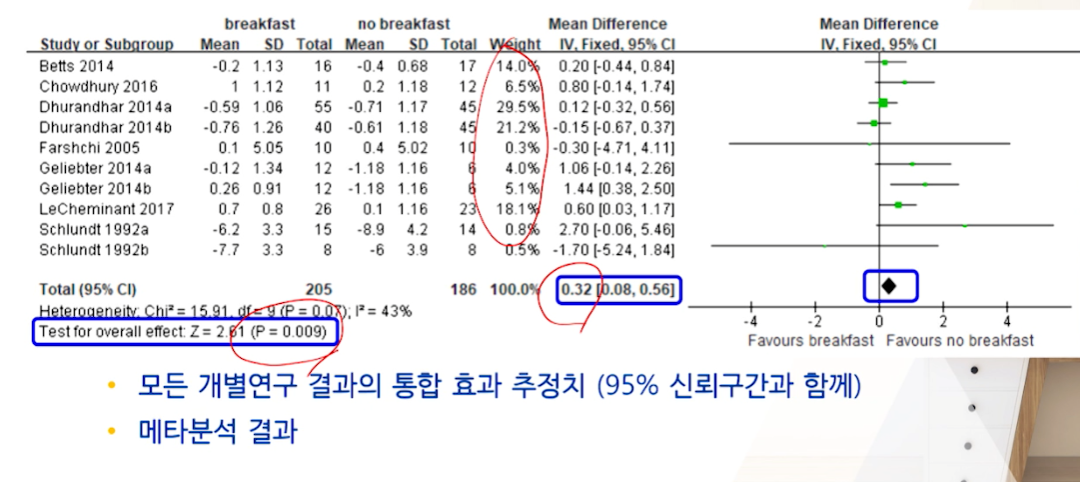
-
MD가
-
결과적으로 아침식사 먹지 않는 것이 체중감량에 더 좋다.
03 이질성 확인
- 일반적인 통계와 달리 p-value가 나오더라도 2가지 평가를 추가해서 확인해야한다.
- 그 중 하나가 이질설 평가
이질성(Heterogeneity)
-
뭐가 다르다 -> 뭐가 다르냐?
- 스터디마다 뭔가가 다르다.
-
메타분석에서의 이질성(Heterogeneity)
- 메타분석에 포함된 개별 연구들의 결과간 변동이 표본추출 오차 이상으로 - 관찰되어 우연으로 설명할 수 없는 것을 뜻함.
- 이질성 발생원인
- 임상적 다양성 : 연구집단, 중재법, 결과 등의 다양성
- 방법론적 다양성 : 연구유형과 bias 위험의 다양성, 치료효과 크기의 방향과 크기의 다양성 등
-
이질성 평가방법
-
그래프이용 : 숲그림(forest plot), L’Abbe plot, Galbraith plot- 일반 통계보다 데이터수가 작으므로 그래프로 나타내는 것을 선호함
-
통계적인 검정: 카이제곱 검정법(Q statistics)과 Higgin’s I2 statistic
-
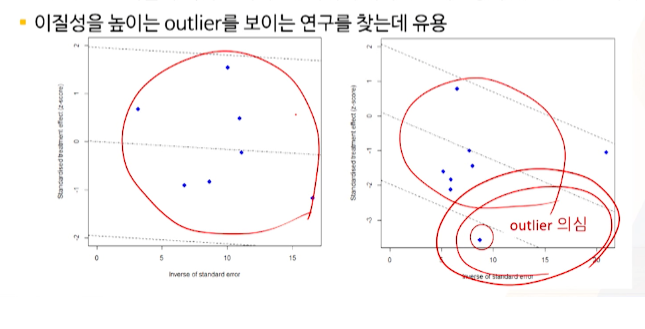
이질성: 그래프를 이용한 시각적평가(1) - 연속형 outcome
-
Forest plot을 통해 개별 연구들의 치료 효과값의 방향성과 신뢰구간이 겹치는지를 검토할 수 있음
-
왼쪽 그림은 combined된 결과에 오밀조밀 잘 모여있지만, 오른쪽 그림은 퍼져있다.
- 오른쪽 그림은 이질성이 발생했다고 의심한다
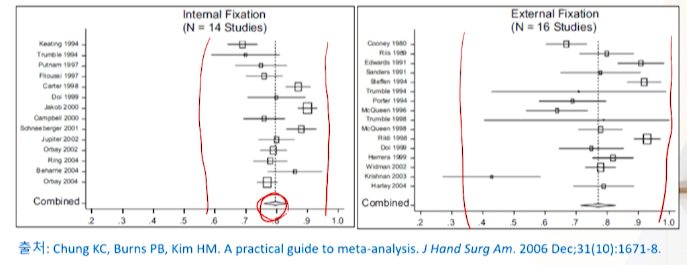
- population을 넓게 설정했거나
- invention을 다양하게 설정했거나 등
- 오른쪽 그림은 이질성이 발생했다고 의심한다
이질성: 그래프를 이용한 시각적평가(2) - binary outcome
-
binary outcomt에 대해 이질성을 의심할 때,
L’Abbé plot(라비 플랏)을 활용할 수 있다. -
대조군 vs invention군에 대해 사건 발생 비율을 계산할 수 있다.
- 발생 비율을 scatter plot으로 그렸을 때 45도 곡선에 있으면 괜찮으나
- 아래 그림처럼 placebo군인데 사건발생율이 너무 다양해버린다.
-
(intervention군이면 이해를 하겠는데) intervention을 안한 군인데 사건발생율이 천차만별로 다양해버린다면 -> population이 다양했을 것이다. -> 이질성이 존재할 것이다.
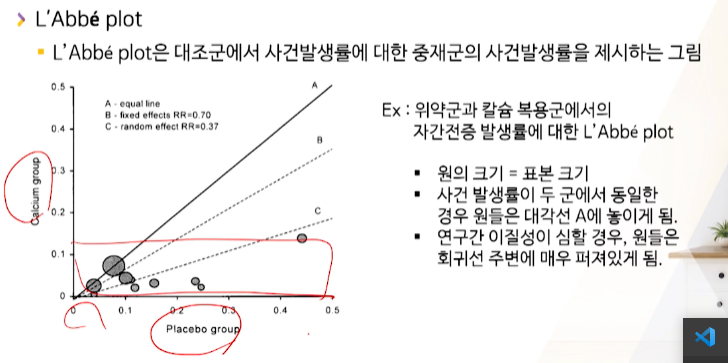
-
(intervention군이면 이해를 하겠는데) intervention을 안한 군인데 사건발생율이 천차만별로 다양해버린다면 -> population이 다양했을 것이다. -> 이질성이 존재할 것이다.
이질성 : 통계적 검정방법
- 그래프의 해석은 주관이 들어갈 수 밖에 없다.
- 내가 보기엔 outlier아닌 것 같은데? 등...
-
이럴 때, p-value가 나오는 이질성 평가를 할 수 있다.
- forest plot 그릴시 무조건 따라오는 결과다.
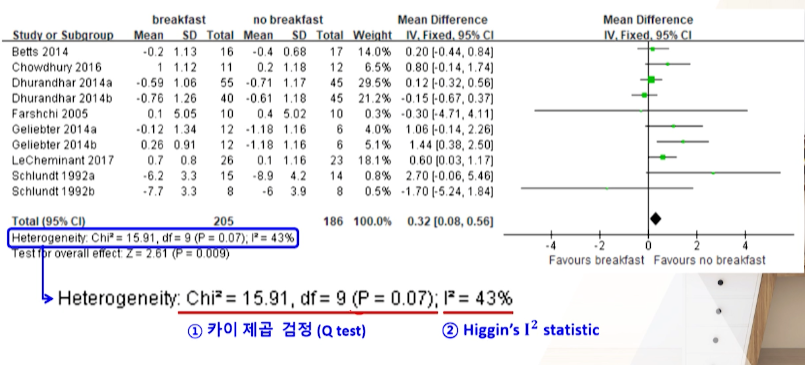
- forest plot 그릴시 무조건 따라오는 결과다.
-
2가지 요소가 있다.
- 카이제곱 검정
- I^2
카이제곱 검정(Q statistics)
-
우리가 아는 카이제곱 검정은 아니다. 카이제곱 분포를 이용한다고 해서 붙여진 이름이다.
-
각 개별 연구들의 중재효과가 산출된 공통 중재효과값으로부터 얼마나 멀리 떨어져 있는지 검정하는 방법
-
H0: 각 연구들은동질하다. vsH1: 각 연구들은이질적이다.- 검정력이 부족해서 0.05가 아닌
0.1로 잡는다.
- 검정력이 부족해서 0.05가 아닌
- P-value > α=0.10 ➔ 귀무가설 채택 ➔ (이질적인 내용 반영 없는) 고정효과모형의 메타분석 수행
-
P-value < α=0.10 ➔ 귀무가설 기각 ➔ (이질적인 내용 반영하는) 변량효과모형의 메타분석 고려
-
카이제곱 검정의 단점
- 연구들이 작은 규모이거나 포함된 연구의 수가 적을 때 검정력이 부족하게 되어 유의하지 않은 결론을 도출하기 쉬움.
- 카이제곱 검정을 시행할 경우 유의수준을 5%보다는 10%로 설정하여 동질성 검정을 시행하는 것이 일반적
이질성이 있는 경우의 해결책 3가지
-
변량효과 모형의 사용- 주로 설명될 수 없는 이질성에 대해 일차적으로 시도될 수 있음.
- 연구들간의 이질성을 통합하기 위해 사용될 수 있지만, 이것은 이질성의 원인을 밝히는 철저한 조사방법은 아님.
-
Subgroup analysis: study가 굉장히 많은 경우, sub group으로 나눠서 분석- 연구들간의 이질성을 해석하기 위해서 동질할 것으로 예상되는 subgroup analysis을 나누어 분석함.
-
메타 회귀분석(Meta Regression)
- 각 개별연구들의 효과크기를 종속변수로, 이질성을 일으키는 연구수준의 공변량을 독립변수로 고려한 회귀분석
- 이질성을 일으키는 공변량을 파악하거나 이를 보정한 통합 효과크기를 추정하기 위함
변량효과 모형의 사용
- Fixed -> Random 효과 모형으로 바꾸니
- total MD가 더 커졌다.
-
똑같은 data지만 이런 효과가 발생하는 이유는?
- study간의 변동 반영 -> 더 보수적인 결과가 나올 수 밖에 없다. -> 신뢰구간이 더 넓어진다.
- 더 board한 상황에서도 결과가 유의하게 나오면 신뢰할 수 있다.
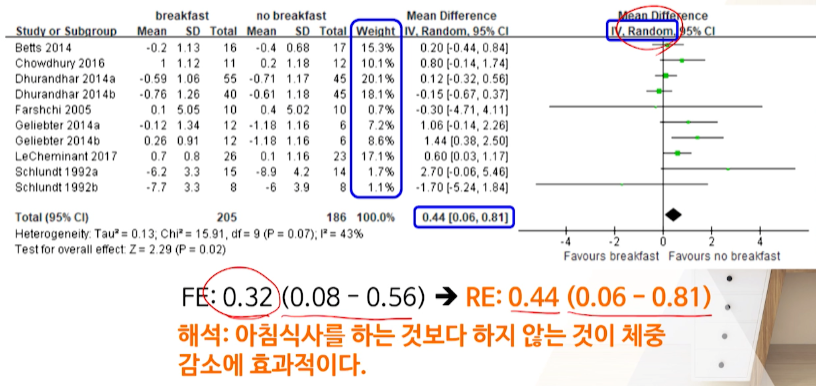
-
요즘은 이질성 없을 경우 FE = RE이니 RE만 제출해라. 보수적으로 볼 것이다. 라는 경향이 있다.
- 하지만, 초보인 우리는 이질성 발생시 FE -> RE로 바꾸는 연습을 하고 있다.
-
FE -> RE로 바꿔서 봤는데도, 결과는 유의하다 -> 아침식사 안하는 것이 체중감소에 더 효과적이다(MD차이 커짐)
04 Publication bias 확인
- 환자 데이터를 직접 다루는게 아니라 이미 발표된 자료를 가지고 분석하다 보니, 연구 결과가 어떻게 출판되느냐에 따라서 발생하는 것이
리포팅 바이어스이고 그 중 대표적인 것이퍼블리싱 바이어스 -
Reporting bias : 연구 결과의 확산이 결과의 특성과 방향에 영향을 받을 때 발생하는 bias
- 가장 대표적인 종류 : publication bias
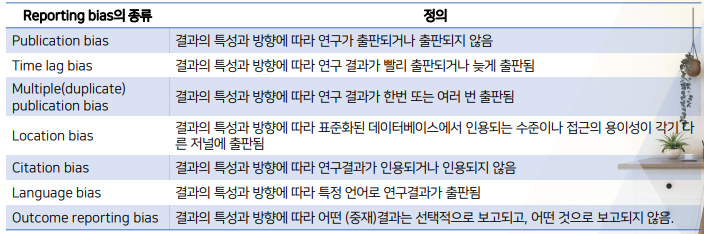
- 가장 대표적인 종류 : publication bias
-
location bias: 2개 검색엔진(mebdline + embase)을 다 이용하면 미국+영국 다 반영되서 없어진다.
-
language bias: 영어 출판 한정 문헌 검색 -> 한/중/일 연구가 바뀐다.
- 한의학이면 한/중/일 검색엔진 다 검색해야한다.
-
publication bias:- 아무래도 positive result가 나와야 출판될 가능성이 높으니, negative result가 나올 데이터들을 빼버리고 메타분석 하게 된다.
Publication bias를 검토하는방법
- 그래픽 vs 테스팅
-
Funnel plot(깔떼기)
- weight가 큰 large study들이 깔데기부분에서 무게를 잡고, small study들이
좌우로 positive/negative result의 대칭을 보이는지- 좌우대칭이 잡히면 bias가 없다
- 오른쪽 그림처럼 오른쪽이 뻥 뚫리면 publication bias가 있다.
- positive result로만 분석해서 비대칭형이 발생한다.
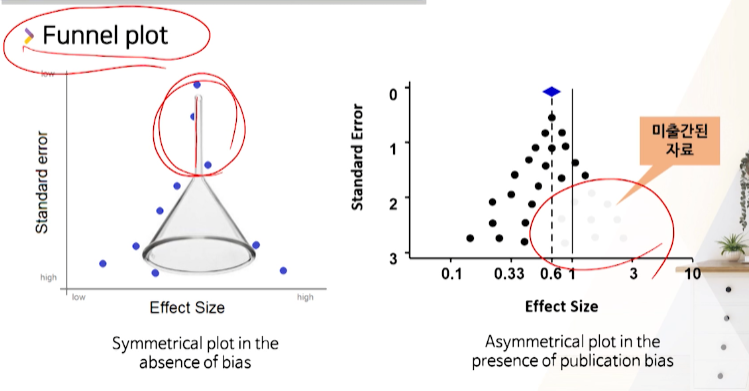
- positive result로만 분석해서 비대칭형이 발생한다.
- weight가 큰 large study들이 깔데기부분에서 무게를 잡고, small study들이
-
Contour-enhanced funnel plots
-
통계적으로 유의한/유의하지 않는 영역을 나눠서, 혹시 유의한 결과만 존재하지 않는지 확인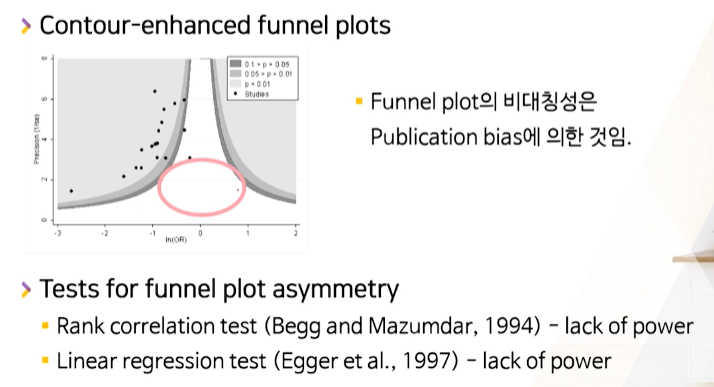
- 그래프로 보는 방법은 study수가 10개이상으로 많아야한다. + 주관적 해석이 들어간다.
-
- Tests for funnel plot asymmetry
- Rank correlation test (Begg and Mazumdar, 1994) - lack of power
- 상관계수를 계산해서, 상관관계가 없으면 좌우대칭
- 상관관계가 존재하면 bias가 존재한다고 한다.
- 전용 프로그램을 사용해야만 됨.
- 보통은 그래프만 이용함
- Linear regression test (Egger et al., 1997) - lack of power
- Rank correlation test (Begg and Mazumdar, 1994) - lack of power
Publication bias의 처리 방법
- Largest study들만을 분석
- study가 아주 많을 경우, 깔데기 손잡이 부분의 논문 수가 많을 때.(사실상 못 쓰인다.)
- Cumulative meta analysis
- 누적시키면서
- Rosenthal.s .file-drawer. method (fail-safe N )
- 미출판 논문의 수를 예측하는 모형사용(Glesser & Olkin, 1996)
- Trim-and-Fill method 사용 (Duval & Tweedy, 2000)
- Copas 선택 모형(Copas, 1999)
- 회귀기반 접근법(Stanley, 2008)
Trim and Fill method
- 제일 많이 사용하는 방법
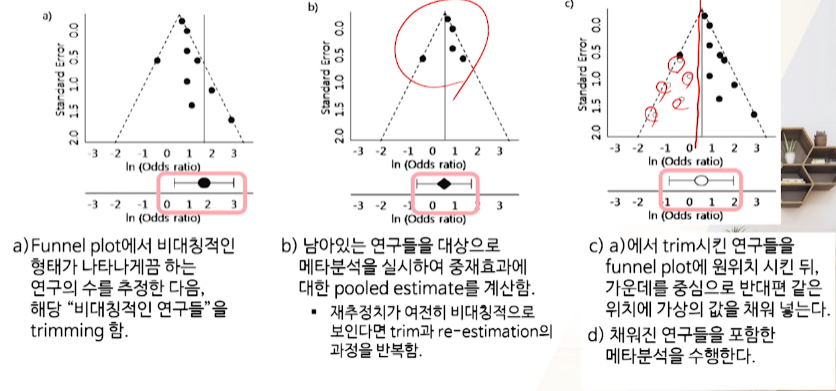
- a) 는 굉장히 비대칭형이다
- b) 대칭형이 될때까지 잘라낸다.
- c) 다시 잘라낸 스터디들을 채우면서 & 데칼코마니로 아직 출판되지 않은 가상의 negative study들을 채워서 메타분석한다.
- 예시
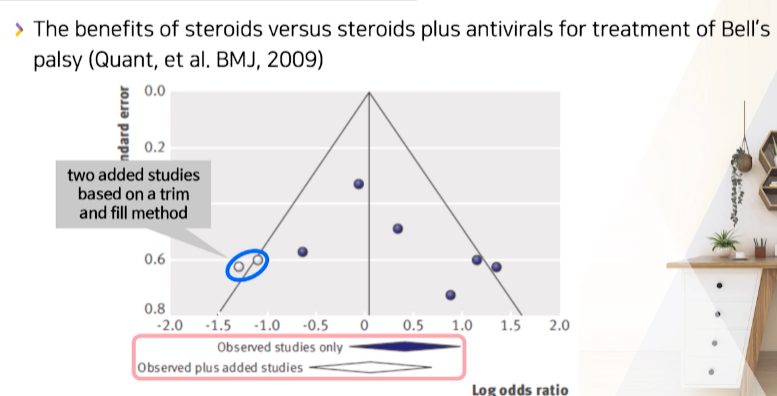
- 스테로이드 vs 안티바이러스제 비교 논문
- 여기서도 가상의 negative study 2개를 fill했다.
- 통계적 유의성은 더 사라졌다?!
Network Meta-analysis(가볍게)
- evidence를 만들어야하기 때문에 왠만한 연구는 전통적 메타분석이 다 이루어졌다.
-
2군의 메타분석 -> 간접적인 중재도 대조군과 비교해서 여러 연구를 네트워크 메타분석
-
예시: 코로나의 치료제는 다양하게 있는데, 어떤 치료제가 mortality나 ventilation에 효과가 좋은지 네트워크 메타 분석을 시행함

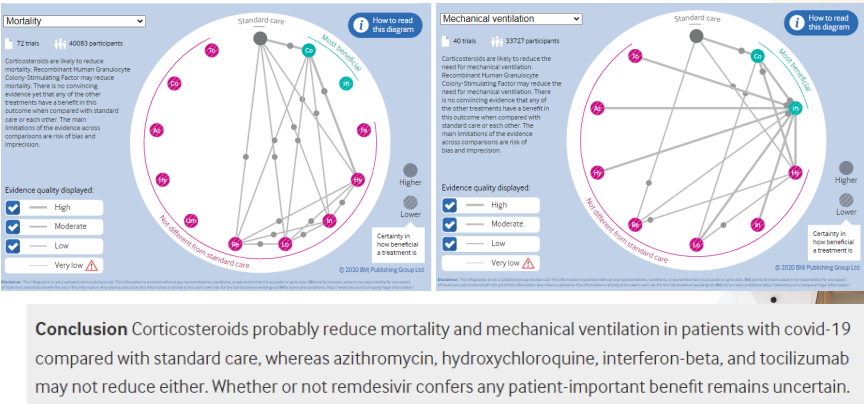
- 초록색 2가지 study가 효과가 좋고 - 빨간색들은 효과가 별로 없다.
진단검사에 대한 메타분석
-
진단의 정확도가 얼마나 정확한지
- 민감도+특이도를 결합시킨 메타분석
- summary Roc를 이용해서 종합적으로 봄
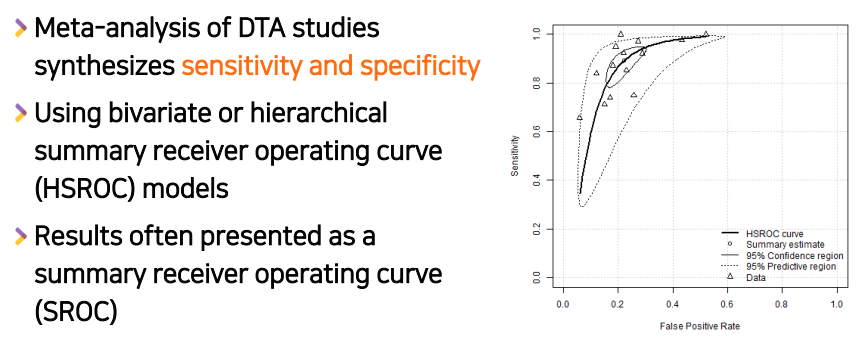
-
예시
- 위쪽 민감도/ 아래쪽 특이도
- 특이도는 비슷한데 민감도는 3번째 검사의 민감도가 제일 좋다고 밝힌 메타분석

- 중재군vs대조군 -> 여러가지 치료군에 대해.. 확대된...
정리하기
-
메타분석은 체계적 문헌 고찰 수행과정에서 2개 이상의 개별 연구의 요약 통계량을 합성함으로써 해당 중재법의 통합된 가중평균 요약 통계량을 정량적으로 산출하여 임상적 효과성을 평가하기 위해 사용되는 통계적 기법이다.
-
메타분석은 메타분석이 가능하다고 판단되는 경우에 수행하는 것이지 체계적 문헌고찰에서 필수적으로 수행하는 것으로 생각해서는 안되며, 연구 대상군, 중재법, 중재결과가 충분히 동질한 경우에 수행하는 것이 바람직하다.
-
메타분석은 개별 연구의 요약 통계량을 계산하며, 각각의 연구에 가중치를 부여한다. 가중치는 많은 정보를 제공하는 개별 연구에 더 많은 가중치를 부여하며, 가중치가 부여된 평균(weighted average)을 계산하여 통합 요약통계량을 산출한다.
-
요약통계량을 결합하기 위한 메타분석의 통계모형에는 고정효과 모형과 변량효과 모형 두 종류가 일반적으로 사용된다.
-
이질성(Heterogeneity)이란 메타분석에 포함된 개별 연구들의 결과간 변동(variation)이 표본추출 오차 이상으로 관찰되어 우연으로 설명할 수 없는 것을 의미하며, 이에 대한 확인 및 평가가 이루어져야 한다.
-
메타분석은 출판된 연구들만을 통합할 경우 치료효과를 과대 추정할 위험이 있기 때문에 출판 비뚤림(publication bias)에 주의를 기울여야 한다.