상관관계를 제는 측도와 바이어스
- 위험요소 <-> 질병간의 상관관계는 산점도로 나오는게 아니다
- risk개념을 알고 -> RR/OR을 통해서 상관관계를 젠다

상관관계를 제기 위해서는 Absolute risk 및 이와 비교하는 메져(RR(Relative risk) & OR(odds ratio), Attributable risk)들이 필요하게 된다.
bias: 상관관계 및 인과관계를 추론할 때 쓰이는 3가지 개념 중 첫번째 개념이다.
- 나머지 2 개념은 다음시간에 알아본다.

Absolute risk

incidence(특정기간, 인구집단내, 새롭게 질병발생, 환자 비율)와 비슷한 개념이다.
- 비율이라 보통 1000명당, 10만명당 으로 표현된다.
Absolute risk: 말그대로 질병이 발생할 0~1사이의 확률
- incidence와 비슷해보이나 incidence: 확률에 x (단위)명당 개념 -> 주로 양수? vs Absolute risk: 0~1사이의 확률
- 줄여서 Risk라고도 하니 Risk는 질병발생 확률(0~1사이)이다라고 생각하자
- incidence와 달리 특정기간이 없이 생략되기도 한다. risk도 기간을 명시하는게 원칙이긴 하지만 생략됨.
  - 예) "어떤 위험에 노출된 이후 -> 3년내 이 질병이 발생할 리스크(확률)" -> 3년내 가 생략된다
    - 특정기간이 없는 리스크는 시간을 따지지 않고, 아무리 오래걸리더라도 1번이라도 발생될 확률로 해석 하면 된다.
- 근본적으로 같은 개념이다. incidence의 몇명당의 개념 때문에 단위가 차이나 보일 뿐
  - 예) "어떤 집단에서 어떤 질병의 risk가 0.003이다"
    - risk는 0.003으로 0~1사이 확률이지만
    - 1000명당으로 보고 X 1000 하면 양수 3이 된다. -> incidence는 1000명당 3명이다.
  - incidence = risk X 단위사람 수로 생각하면 된다.

Absolute risk 계산 예제

위험요소 - 질병에 대한 Risk를 계산하기 위해서는
- 위험요소 노출시 risk(확률)
- 위험요소 노출X시 risk(확률) 2CASE를 각각 구해서 비교한다
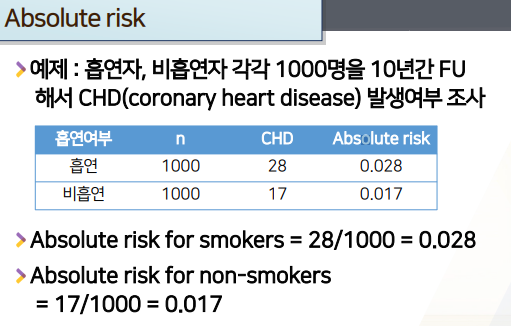
흡연자 1000 | 비흡연자 1000명 각각 찾아서, 10년간 FU(팔로우업)해서, CHD(관상동맥질환) 발생여부를 조사했다
- 흡연자 1000명 중 28명 CHD 발병 -> 흡연자의 Absolute risk(확률) = 28/1000 = 0.028
- 비흡연자 1000명 중 17명 CHD 발병 -> 비흡연자의 Absolute risk(확률) = 17/1000 = 0.017

질병과 위험요소의 상관관계 계산을 위한 Risk비교

위험요소와 질병의 상관관계를 조사한다?
- == 위험요소 노출 -> 질병 Risk vs 위험요소 노출X -> 질병Risk 각각 구해서 비교해야한다.
- 위험요소의 (O/X) 2Case 모두에 대해 -> 질병 발생여부(O/X)를 조사 -> 각각의 Risk(확률) 계산 -> 비교를 해야한다
  - 흡연자(위험요소 노출)의 CHD(질병) 발생여부를 통한 Risk계산
  - 비흡연자(위험요소 노출)의 CHD(질병) 발생여부를 통한 Risk계산
위-질 상관관계를 위한 -> 위험요소 노출 Risk vs 위험요소 노출X Risk의 2case Risk비교 -> 2가지 비교법이 있다.
1. 상대적 비교
  1. relative risk (RR) = risk ratio
  2. odds ratio (OR)
2. 절대적 비교
  1. risk difference (RD) = attributable risk(역학)

RR & OR

질병과 위험요소의 상관관계를 위한 상대적 risk비교
임상paper에서 rr보다 OR이 더 자주 등장한다.
- OR은 몇이고, 해석을 하면 어떻다
- OR을 설명해보라고 하면 잘 못하는 사람들이 많다.
이번 강의에서는 개념을 읽히고, 다음 강의에서는 스터디별로 계산법을 배운다.

Relative risk (RR)

RR: (분자:)위험요소 노출 됬을 때 질병발생확률(risk)이 / (분모:)위험요소 노출X일때 질병발생확률(risk)의 몇배인가 -> 노출시 질병발생확률risk가 몇배냐
- 공식도 단순하다. 위험요소 노출X 질병발생 확률(risk)이 분모

RR해석
- 1을 기준으로 분자 or 분모 더 큰 것에 집중
  - RR>1 분자가 더 큰 경우:위험요소 노출 O 일때가 질병발생확률(risk)이 더 높다 -> 노출시 risk 높으면 양의 상관관계가 있다. or 노출X시 risk가 높으면 상관관계 음으로 있다.
  - RR<1 분모가 더 큰 경우:위험요소 노출 X 일때가 오히려 질병발생확률(risk)이 더 높다 -> 노출안될 시 risk 높으면 음의 상관관계가 있다
    - 반대면 상관관계 없는 것이 아니므로 조심
- 1이면 노출O, 노출X risk같다 -> 아예 상관관계 없다
RR=1 : 위험요소 노출됬을 때와 / 노출되지 않았을 때의 질병발생확률이 같다
- 위험요소 <-> 질병발생확률(=질병발생여부)와 관계가 별로 없다
- 노출되든 말든 발생확률이 동일하니까
- 랠러티브 리스크가 1에 가깝다 -> 상관관계가 없다
RR>1 : 분자가 더크다 = 위험요소 노출될 때가 질병발생확률(risk)가 더 높다 -> positive association의 관계
RR<1 : 분모가 더크다 = 위험요소 노출되지 않았을때가 오히려 질병발생확률(risk)가 더 높다 -> negative association, protective effect
- 최종 해석은 위험요소 노출시 낮아진다로 해석하자
- 반대로 분자인 위험요소 노출 시가 ->질병이 덜 발생한다 -> 위험요소라고 했지만 오히려 반대로 낮춰주는 보호 효과

RR 예시

앞에서 Absolute Risk를 구했었다. -> 그냥 risk로서 RR계산시 사용된다.
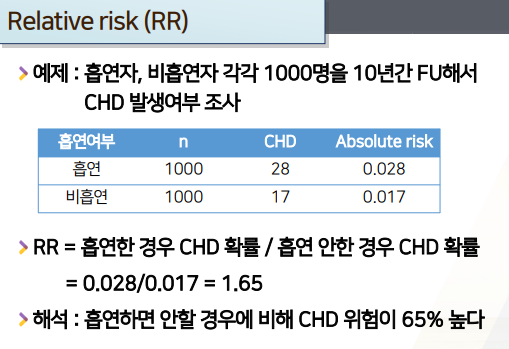
- RR은 분자 = 흡연(위험요소 노출)시 risk = 0.028 / 0.17 = 분모 = 비흡연시(위험요소 노출X) risk 로 계산한다
- RR(=1.65) > 1 해석
  - 분자가 더 크다 -> 위험요소 노출시가 질병발생확률(risk)가 더 높다 -> 흡연과 CHD는 양의 상관관계다
- RR은 더 큰 위험요소라도 최종적으로는 분자(위험요소 노출기준)기준으로 해석하며 1에서 떨어진 범위의 %만큼 질병 발생 확률(질병 위험)이 % 높/낮다로 해석한다
  - 분자가 크니 = 더 큰 흡연시 1.65에서 65만큼 %를 사용해 -> CHD 위험(질병발생 확률)이 65%만큼 높다
  - 분모가 크다 = 더 큰 비흡연시 0.65에서 1에서 35 -> 질병발생확률이 35%만큼 커진다 -> 흡연시 35%만큼 낮아진다

Odds

RR는 위험요소 노출 case에 따른 2개 risk의 비율(분모가 위험요소노출X)였다.
odds ratio는 risk가 아닌 2개 odds의 비율이므로 odds부터구해야한다.
- odds: 분자 질병발생 확률p(risk)이 / 분모 질병발생 안할 확률(1-risk, 1-p)의 몇배인가
- cf) rr: 위험요소 노출O 질병발생확률 / 위험요소 노출X 질병발생확률의 몇배인가
risk와 odds의 관계
- risk: 질병발생 확률(0~1) 그 자체
- odds: 질병발생 확률 risk(p)가 / 질병발생안할 확률 1-risk(1-p)의 몇배인가
  - risk가 커지면, risk / 1-risk의 odds역시 커지게 된다.
  - p/1-p(0<=p<=1) 그래프를 보면 or p를 조절해보면 oods의 범위는 0(p작) ~ 무한대 사이 값(p커)

Odds ratio(OR)

risk로 odds = risk/1-risk 를 구해놓은 상태에서
- RR와 비슷하게 위험요소 노출O/X case를 각각 분자/분모의 기준으로 놓고 odds 2개의 비율로 odds ratio를 구할 수 있다.
- odds도 위험여부 노출O / 노출X 2 case를 미리 구해놔야 -> odds ratio를 분자/분모 나눠서 구한다
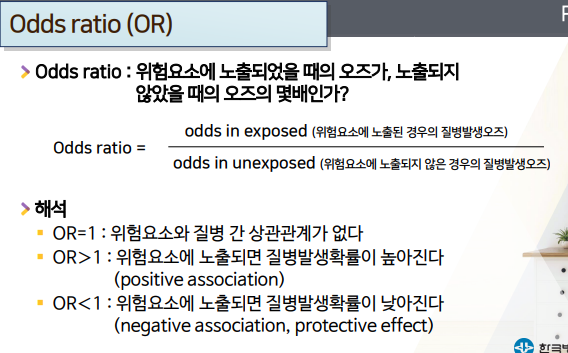
odds ratio: (분자:)위험요소 노출O 일때의 odds 가 / (분모:)위험요소 노출X 시의 odds의 몇배인가
- risk=질병발생확률이 아니라 거기서 나아가 구한 odds가 사용되는 것을 인지하자

OR 해석: risk대신 odds가 사용된 비율이지만, 상관관계 해석은 비슷하다. 왜냐면 risk와 odds는 비례하기 때문에
- OR=1 : 위험요소와 질병 간 상관관계가 없다
  - 분모=분자 같다 -> 위험요소 노출여부와 관계없이 odds가 같다 -> risk도 같다 -> 상관관계 없다
- OR＞1 : 위험요소에 노출되면 질병발생확률이 높아진다(positive association)
  - 분자가 크다 -> 위험요소 노출시 odds가 크다 -> odds크면 risk도 같이 커졌다는 말 -> 위험요소-질병 양의 상관관계
- OR＜1 : 위험요소에 노출되면 질병발생확률이 낮아진다(negative association, protective effect)
  - 분모가 크다 -> 위험요소 노출 안될시 odds = risk가 크다 -> 위험요소-질병 음의 상관관계다
  - 해석 최종은 위험요소 노출시 더 낮아진다로 위험요소노출O로 해석끝낸다

OR 수식정리

p1(p서브원): 위험요소 노출시 risk
p0(p서브제로): 위험요소 노출 안될시 risk
- my) 위험요소 노출여부에 따라 p1/p0로 나눈다
RR = 위험요소 노출여부에 따라 구한 risk 2개 -> 2case risk의 비율 = p1/p0 = 위험요소 노출시 risk는 노출안되시의 몇배인가?
OR = 위험요소 노출여부에 따라 구한 risk 2개로 -> 위험요소 노출여부에 따라 구한 odds 2개를 계산 -> 2case odds의 비율

OR(Odds Ratio) 예시

위험요소 노출O/x에 따른 risk 2개(질병발생확률)가 구해졌는지 확인
- 문제에서 주어져있다.
- 각 risk = (위험요소 노출 O 및 X에 대한 새롭게 질병발생자 수 / 인구 수)
risk 2개로, 각각(위험요소 노출O 및 X)의 질병odds 2개를 구한다
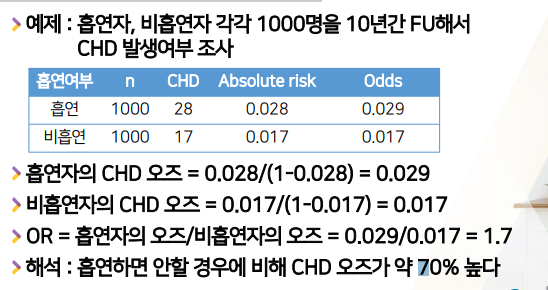
1. 위험요소 노출시 odds = 흡연시 질병(CHD)odds = 흡연시risk / 1-흡연시risk
  - 0.028/(1-0.028) = 0.029
2. 위험요소 노출X시 odds = 비흡연시 질병(CHD)odds = 비흡연시risk/1 - 비흡연시risk
  - 0.017/(1-0.017) = 0.017
질병odds 2개로 위험요소 노출 Odds가 /위험요소노출X Odds의 몇배냐로 나눠서 구한다.
- 흡연자 오즈 / 비흡연자오즈 = 0.028 / 0.017 = 1.7
OR해석: 혹시 1보다 작아도 결국엔 분자 위주로 해석(위험요소 노출시 질병발생여부는 n배)
- OR > 1.7: 흡연을 하면, 안할경우 비해, CHD Odds가 1.7배이다
  - 흡연을 하면, 안할경우 비해, (1보다 멀어진만큼인 0.7을 보고) CHD odds가 70% 더 높다

RR vs. OR

랠러티브 리스크(RR)은
- 해석이 직관적이다 -> 질병 발생 확률(0~1)의 (위험요소 노출에 대한 O/X)비율이니까(위험노출시 몇배 더 발생하냐?) -> 이해가 잘된다
- 그러나 스터디 종류에 따라서 추정이 불가능한 경우가 있다.
  - 즉, bias없는 추정치를, 얻을 수가 없는 경우가 있다.
  - 예를 들어, case-control study가 그렇다.
오즈 레이시오(OR)은
- 질병 발생 확률의 비율(몇배?)가 아니라 오즈라는 개념을 한번 더 이용해야하므로 직관적으로 와닿지 않고 해석이 어렵다
- 그런데도 불구하고, OR이 훨씬 더 많이 임상논문에서 사용/보고된다.
  - OR은 수학적으로 굉장히 좋은 성질을 가지기 때문
    - 매쓰매틱스 미라클 현상을 보여주기도 하고, 어려운 수학문제를 간단하게 만들어주는 성질이 있다.
    - case-control 같은 경우도, RR 추정자체가 불가능한데, OR은 추정할 수 있다.
    - 즉, 스터디 종류를 타지 않고 다 사용된다
다행인 점은
- 질병발생 확률(risk)가 작은 경우에는 RR==OR이 비슷한 성질이 있다.
  - 예시도 RR = OR처럼 나왔다. risk가 너무 작은 값인데, 소수2까지 반올림하니 같아졌음.
  - 아주 흔한 질병인 고혈압, 당뇨가 아닌 경우라면,대부분의 질병이 질병발생 확률(risk)이 낮다. == 스터디 디자인 때문에 RR이 추정되지 않아도 OR을 쓰면 된다.
- 공식에서 보면, Odds = p1/1-p1 or p0/1-p0에서, p가 아주 작아진다면 -> 분모는 1에 가까워지고 -> 값 자체는 p1 or p0로서 risk에 가까워진다.

Attributable Risk

위험노출된 개개인(흡연자)에 인터벤션(금연보조제) 작동시, 얼만큼의 질병risk감소 효과가 있을까?라는 질문에 대한 답을 AR(e)로 구한다.
- 위험노출된 개개인(흡연자)에 인터벤션(금연보조제) 작동시, 얼만큼의 질병risk감소 효과가 있을까?
- 위험노출된 개개인(흡연자)에 인터벤션(금연보조제) 작동시, 얼만큼의 질병risk감소 효과가 있을까?
- 위험노출된 개개인(흡연자)에 인터벤션(금연보조제) 작동시, 얼만큼의 질병risk감소 효과가 있을까?
risk비교 중에 위험요소 노출o/x 집단간 상대적 비교가 아니라 절대적 비교 메저다
예를 들어 인터벤션을 1개 생각해보자. ex> 금연보조제(intervention)
- "금연보조제는 -> 흡연 - CHD위험을 얼마나 줄일 수 있을까?"
  - "흡연하던 사람이, 금연을 하면, CHD위험이 얼마나 줄어들까?"와 같은 질문이다.
- 즉, intervention으로 위험요소 노출 -> 노출X의 상황으로 만들었을 때, 질병위험을 보는 것이다.

일단 인터벤션 작용 전에 위험요소(흡연자)-질병(CHD)위험의 구성 모델을 쪼개서 생각해본다.
- 흡연자 - CHD위험: background 질병risk + 흡연 때문에 증가하는 질병risk
  - 위험요소 노출(흡연)과 관계없는 background risk도 있다.
  - 여기에 위험요소 노출을 통해 risk를 더 올린다.
인터벤션 금연보조제이 작용해서 risk를 줄일 수 있는 부분은 흡연 때문에 증가하는 질병risk부분만 해당한다.
- 금연보조제로 금연을 하더라도, background risk는 줄이지 못한다.

다시 정리해보면, 위험요소에 노출된 사람의 질병위험 =
1. background risk(노출되지 않은 사람의 질병위험)
  - 밑에 그래프에서 오른쪽 초록색 부분
2. 위험요소 노출 때문에 증가하는 risk
  - 위험요소 노출 질병위험은 = background가 기본으로 있고 + 위험요소노출 때문에 background에서 추가로 떠안은 질병위험을 더 떠안게 된다.
인터벤션으로 줄일 수 있는 risk = 위험요소 노출 때문에 background risk에 추가로 떠안은(증가된) 질병위험 부분이다.
- = 위험요소 노출된 사람의 (전체)질병위험 - background risk(노출되지 않은 사람의 질병위험)
- = 예방을 통해 달성할 수 있는 포텐셜
my) 위험요소 노출 risk != 위험요소 노출 때문에 증가된(background에서 추가된) risk
my) background risk = (말은)위험요소에 노출되지 않은 경우의 risk = (뜻은) 위험요소 때문에 증가한게 아니라 원래 가지고 있는 risk

Attributable risk (among the exposed) = ARe = risk difference (RD)

Attributable risk는 아래 개념 때문에 등장한 개념이다.
- 위험요소 노출된 사람의 (전체)질병위험 - background risk(말은, 노출되지 않은(노출과 상관없이 가지는?) 사람의 질병위험)
among the exposed는 노출된 사람에 한하여 Attributable risk를 계산한 다는 것이다.
- 그렇다면, 교재의 위험요소에 노출되지 않은 사람의 질병위험 = 노출여부에 상관없이 background로 가지는 질병위험이라는 뜻이겠다.
- among the exposed가 안붙는 Attributable risk도 뒤에 다룰 것이다.
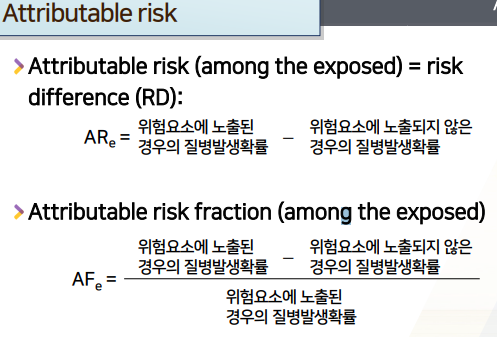
ARe(xposed) = RD(Risk Diferrence) =
- 위험요소에 노출된 경우의 질병발생확률 - 위험요소에 노출되지 않은 경우의 질병발생확률
  - 이라고 표기하지만
- 위험요소 노출된 경우 risk(default background risk 포함된 전체risk) - 위험요소 노출되지 않은 경우 risk(background risk)
- = 위험요소 때문에 (background risk에)추가적으로 떠안게 된 risk

Attributable risk fraction (among the exposed) = AFe

ARe = 위험요소 노출 때문에 (background risk에)추가적으로 떠안게 된 risk자체를 report하기도 하지만
AFe로서 ARe / 위험요소 노출된 경우 risk(default background risk 포함된 전체risk)를 나눠서(전체 중 일부를 나누는 것)
- (bg risk포함)위험요소 노출 전체 risk 중 위험요소 노출 때문에 추가적으로 떠안게 된 risk는 전체 중 몇%를 차지하는 가를 의미하는 것을 사용하기도 한다
예를 들면, 흡연자로서 가지고 있는 전체 CHD risk 중 흡연 때문에 떠안은(증가된 risk는 몇프로를 떠안은 것인가 -> AFe로 계산한다

AR, AF 수식 정리

ARe = RD로서 risk차이 = 전체risk - backround risk로 계산
- 뭐야.. 전체 risk라고 생각했던 것이 위험노출시 risk = p1이고
- background risk는.. 진짜 위험노출 안됬을 때의 risk= p0였네...
  - 까고보면,, p1 = p0(background risk) + @(추가로 떠안은risk)겠지?
  - 일단 background risk = p0로 계산하는 것을 외워두자.
AFe = ARe=RD=risk차이=p1-p0로 계산 해놓은 상태에서
- ARe / p1로 p1자체를 전체risk로 생각하고 나눈다
- (p1-p0)/p1
- 해석: 전체인 p1 중에 attributable risk가 몇프로를 차지하는가?

Attributable risk 예시

구하고자 하는 것은: 흡연 때문에 증가한 Attributable risk = ARe = RD = risk차이 = 흡연 때문에 떠안은 risk 및 전체 risk에서 그 것의 비율(%) = AFe = ARe/p1

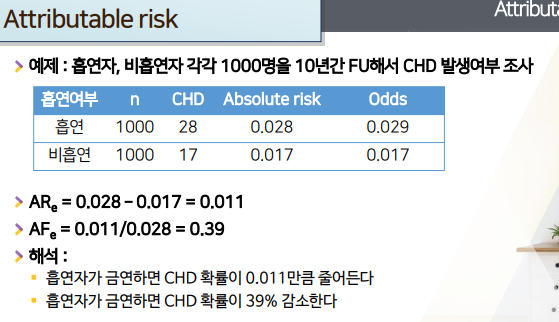
risk 2개를 구한다.
- 흡연(위험노출): 28/1000 = 0.028 (p1 = 전체risk)
- 비흡연(위험노출X): 17/1000 = 0.017 (p0 = background risk)
risk 2개의 차이(p1-p0)가 ARe(RD)다
- ARe = 0.028 - 0.017 = 0.011
ARe(RD)를 전체risk(backgroud + RD)를 의미하는 p1으로 나눠 위험요소로 인해 떠안은(증가한) risk는 전체risk의 몇퍼를 차지하는지를 AFe를 구해서 본다.
- AFe = ARe / p1(전체risk) = 0.011 / 0.028 = 0.392 -> 39%
해석:ARe, AFe는 인터벤션이 작동하여 위험요소 노출O->X가 되면, 감소되는 risk로서 해석하자.
- ARe, AFe = 절대적 비교 -> 인터벤션이 나타날 차이
1. 흡연자 금연하면 CHD확률이 0.011(ARe)만큼 줄어든다.
2. 흡연자 금연하면 CHD확률이 39%(AFe*100) 감소한다

Attributable risk for the population = ARp or PAR

ARe: 위험노출된 개개인(흡연자)에 인터벤션(금연보조제) 작동시, 얼만큼의 질병risk감소 효과가 있을까?
ARp: 위험노출된 커뮤니티(도시)(의 흡연자들)에 인터벤션(금연보조제, 금연 프로그램들을 시민에 제공) 작동시, 얼만큼의 <도시전체 incidence> 감소 효과가 있을까?
- 예시:“시청에서 성공적인 금연 프로그램을 제공하면 도시 전체의 CHD incidence는 얼마나 낮아질까?”

도시 전체의 CHD incidence(risk?)도 개개인처럼 total risk(p1)과 background risk(p0) -> 그로 인해 구하는 위험요소 때문에 떠안은(증가하는) risk개념이 있을 것이다.
- 도시 전체의 CHD incidence = background incidence + 흡연 때문에 증가하는 incidence
  - 흡연을 안해도 기본적으로 CHD는 발생한다 = bg incidence가 있다.
- 흡연 때문에 증가하는 incidence만큼이 시청 금연프로그램(인터벤션)이 줄일 수 있는 risk의 potential이다
계산시 주의사항:
- 도시든 커뮤니티든..간에 모든사람이 위험에 노출되진 않는다. -> 비흡연자가 포함되어 있을 것이다. but 시청 금연 프로그램 = 인터벤션은 위험노출 O(흡연자)에 대해서만 CHD risk를 줄인다.
- 즉, 파퓰레이션 = 흡연자 + 비흡연자로 구성되어있다.
  - 만약, all 비흡연자라면 인터벤션인 금연프로그램 효과는 0으로 나올 것이다.
  - 흡연자가 많았다면, 인터벤션인 금연프로그램 효과가 크게 나올 것임.
인구집단 전체(도시, 국가...)의 질병위험 = background risk + 위험요소노출 때문에 증가하는 risk
- 인구집단 전체의 관점에서 위험요소노출 때문에 증가하는risk =
- 인구집단 전체의 질병위험 – 위험요소에 노출되지 않은 사람의 질병위험(bg로 추정)
  - : potential for prevention 달성할 수 있는 예방효과 포텐셜

ARp or PAR 공식

ARp= 인구집단 전체 risk - 위험요소에 노출되지 않은 그룹의 질병발생확률(bg로 추정)
AFp= ARp / 인구집단 전체 risk

ARp or PAR 수식 정리

ARp를 계산하기 위해서는 추가적으로 r위험요소에 노출된 사람의 비율 in 전체 population을 알아야하며, r을 가중평균하여 total risk(p)를 구한다
- 전체인구 중 r만큼의 사람만 위험요소에 노출 되었다고 가정한다면,
- 인구집단 전체risk 계산법은 가중평균(weighted sum)을 이용한다
  - p = p1*r + p0*(1-r) (노출된사람비율r에 대해 p1의 risk를 가지고 있고~)
p를 구했으면 p - p0 (전체rist-노출되지X risk(bg))로 ARp를 구한다.
ARp/p로 AFp를 구한다.

ARp 예제

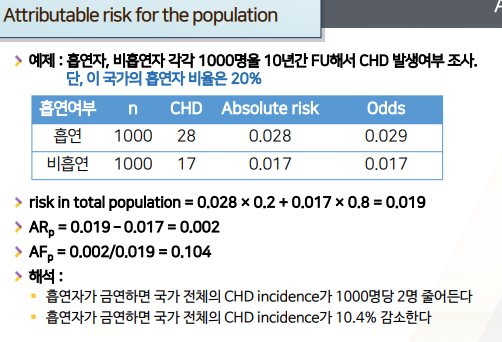
아까와 같은 예제이지만, 단, 이 국가의 흡연자 비율은 20%에서 r = 0.2이며 ARp에 대한 문제임을 알아채야한다
- 국가 레벨에서, Attributable Risk와 Attributable Risk Fraction을 구해보자.

r이 얼만지 확인한다.
- r = 0.2
risk 2개(p1, p0)가 있는지 확인한다.
- 28 / 1000 = 0.028
- 17 / 1000 = 0.017
risk와 r로 가중평균을 통해 p(total risk in population)를 구한다.
- p = p1 X r + p0(1-r) = 0.028 X 0.2 + 0.017 X 0.8 = 0.019 (국가전체의 CHD 위험)
ARp는 p1-p0가 아니라 p-p0로 구한다.
- p - p0 = 0.019 - 0.017 = 0.002
AFp는 ARp(p-p0) / p로 구한다
- ARp / p = 0.002 / 0.019 = 0.104
해석(AR, AF는 인터벤션으로 인해 위험노출X가 된다면, ARp,AFp만큼 risk가 낮아지는 것을 얘기)
1. 흡연자가 금연하면 국가 전체의 CHD incidence가 1000명당 2명 줄어든다
  - 확률이 0.002 -> 소수3째자리의 확률(risk)은 -> X1000한 뒤 1000명당을 붙인다
2. 흡연자가 금연하면 국가 전체의 CHD incidence가 10.4% 감소한다

RR vs AR, Af의 비교 예제

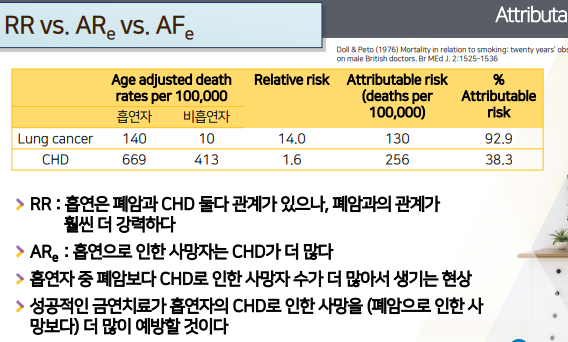
흡연/비흡연자의 10만명당 사망률을 조사했는데, **이것이 계산이 필요한 질병발생확률인 risk가 된다???
- 10만명당 사망률을 == 새롭게 질병발생환자수/인구수인 risk를 미리 계산한 것으로 취급한다
  - 사망률도 risk로 사용될 수 있다.

10만명당 사망률을 risk로 취급해서 보는데, 위험요소O/X 이전에, 질병도 2case 상태라서 -> 질병 1개(Lung Caner)를 먼저 선택해서 보자
- 질병 1개에 대해서 위험요소 노출O/X의 RR, OR, AR 등을 해석해야한다
질병 1개 Lung Caner에 대한 RR은 위험노출O risk가 / 위험노출X risk의 몇배냐 (발생확률의 비율)다.
- RR = risk1/risk0을 계산해야하는데, 사망률 == 미리계산된 risk (새롭게발생환자수/인구수)로 보자.
  - 위험요소노출O risk = 흡연자 사망률 = 140 / 100,000
  - 위험요소노출O risk = 비흡연자 사망률 = 10 / 100,000
  - RR: 140 / 10 = 14(양의 상관관계)
질병 1개에 대한RR의 해석: 기본적으로 발생확률이 몇배냐?를 물어면서 1을 기준으로 상관관계 없다(=)/ 양의 상관관계(>1) / 음의 상관관계 or 프로텍트이펙트(<1)의 상관관계로 해석하기 위해 사용된다.
- 1에서 떨어진 만큼이며 위험요소O기준으로 최종 해석을 만든다.
- (더 큰 분자 = )흡연시 (1에서 떨어진 만큼)140% LungCancer 사망률(원래는 위험)이 높다.
이제 나머지 질병 1개 CHD에 대해서도 RR 계산 및해석한다.
1. risk -> 사망률로 -> 위험O(흡연): 669/100,000 | 위험X(비흡연): 413/100,000
2. RR -> risk1 / risk0 = 사망률1 / 사망률0 = 669 / 413 = 1.6 (양의 상관관계)
3. RR의 해석 -> 흡연시 60% CHD 사망률이 높다

각 질병순으로 AR(더 간단)을 계산해보자.
1. AR = 위험O/X의 risk차이 = 사망률차이 = (p아닌 경우) p1-p0
  - cf) ARp = r로 구하는 전체/위험X의 risk차이 = 사망률차이 = p(by r)-p0
  - LungCancer AR: 140 - 10 = 130
  - CHD AR: 669 - 413 = 256
질병간 RR로 위험요소와의 상관관계 비교 vs 질병간 AR로 실제 값 차이 + 인터벤션적용시 낮아지는 효과 비교를 해석해보자.
- RR: 폐암RR(14.0)이 > CHD RR(1.6)보다 훨씬 랠러티브 리스크가 훨씬 크다.
  - 일단 둘다 1보다 크기 때문에 두 질병 모두 흡연과 양의 상관관계가 있다. (RR=1 상관관계없음)
  - 폐암이 비흡에 비해 흡연의 사망(원랜 질.발)확률이 훨씬 크다.
  - RR이 크다 = 흡연(위험요소)-질병간 상관관계(양)가 폐암이 CHD 더 크다
    - 흡연과의 상관관계가 폐암 > CHD보다 더 강력하다
- AR: 폐암AR(130)보다 CHD AR(256)이 AR이 더 크다.
  1. AR1-실제 값차이는 흡연으로 인한 10만명당 사망자수가 CHD가 더 많다.
  2. AR2-인벤효과로 낮아질 %는 금연시 10만명당 사망자 수(원래risk) CHD가 더 낮아질 것이다.
RR과 AR의 차이가 나타는 이유? 다른 종류의 메저인 것은 맞는데...
- 흡연자 중 폐암으로 사망 보다 < CHD으로 사망하는 수가 훨씬 더 많아서 그렇다.???!!!
  - risk1(p1)이 LungCaner보다 CHD가 압도적으로 많아서 생기는 현상
  - my) 질병간 p1의 실제 값차이가 많이 나면 RR비교/AR비교가 달라진다?
    - my) risk의 비율은 LungCander 압도적 -> RR 압도적이나, 절대적인 수가 CHD비에 딸려서... -> AR(risk비율이 아닌 양차이)은 딸린다.
RR, AR을 통해 알 수 있는 정보
- RR을 보니, 흡연은 폐암과 관련이 많긴 하겠지만(RR=(risk비율)상관관계)
- AR을 보니, 효과적인 인터벤션(금연치료)를 통해 risk(여기선 사망)을 낮출 수 있는 효과는 CHD가 더 많이 낮아춰 -> 효과가 더 좋다(AR=(risk실제갑차이)반대로 인으로 인한 위험노출X가 될 때 risk를 더 줄인다.)
  - 사망 예방효과로서,은 CHD로 인한 사망이 폐암으로 인한 사망보다 더 save될 것이다.

연습문제(RR, OR)

주 3회 이상 운동한 65세 이상 성인은 100명 당 15명에서 당뇨병이 발병하였고, 주 3회 미만으로 운동한 65세 이상 성인은 100명 당 40명에서 당뇨병이 발병하였다고 하자. 다음 중 틀린 설명은?

주 3회 이상 운동’라는 인자에 대한 당뇨병의 relative risk는 0.375이다.
주 3회 이상 운동’라는 인자에 대한 당뇨병의 odds ratio는 약 0.26이다.
relative risk가 1보다 작으므로 주 3회 이상 운동하면 당뇨병 발병 확률이 낮아짐을 의미한다.
odds ratio가 0.26이므로 주 3회 이상 운동하면 당뇨병 발병 확률이 74% 감소함을 의미한다.

RR, OR문제라면,

위험요소 노출O/X를 행으로 주되, RR, OR은 분자가 위험노출여부O이므로 O->X순으로 행을 만든다.
- 위의 문제의 경우 언급되는 것을 위험노출여부 O로 본다. 비록... 주3회이상운동으로 노출X인 것 같지만... 노출O로 본다.

//table template
  //노출여부그룹별  n수 + 질병환자수를 각각 줘서, risk를 a/n으로 계산할 경우
  |노출여부| 전체n | 질병 O | (Absolute) risk | Odds|
  |---|---|---|---|---|
  |흡연|n|a| a/n |r1/1-r1|
  |비흡연|m|b|b/n|r0/1-r0|

  //노출여부그룹별  risk를 바로주거나, risk소수점을 없애려고 x k 해놓은 경우
  |노출여부| k명당 발생자수(risk에 k곱) | (Absolute) risk | Odds|
  |---|---|---|---|
  |흡연|rr1| rr1 / k |r1 / 1-r1|
  |비흡연|rr0|rr0 / k|r2 / 1-r2|

노출여부	k명당 발생자수(risk에 k곱)	(Absolute) risk	Odds
주3회이상운동	15	0.15	0.176
주3회미만운동	40	0.40	0.666

각 노출여부그룹별 risk 2개 계산 -> odds 2개 계산 -> 분자:위험(여기선 주3회이상운동이 기준이므로 위험o로 본다/분모:위험X로 몇배냐?를 1을 기준으로 1에서 멀어진 만큼 % 줘서 생각한다.
- RR: risk1/ risk0 -> 위험노출될 때가 질병발생확률이 몇배냐(비율)?
  - 0.375
- OR: odds1/ odds0 -> 위험노출될 때가 발생비율이 몇배냐?(risk랑 비슷?)
  - 0.264
해석: 1 기준으로 위험노출여부O 하면 ~1에서 멀어진 만큼을 %로 주고 %만큼 높다 /낮다를 말하면 된다.
- RR:0.375 < 1 : 주3회이상운동(위험노출여부O)하면, 0.625x100 = 62.5%만큼 질병발생확률이 낮아진다
- OR: 0.264 < 1: 주3회이상운동(위험노출여부O)하면, 0.736x100 = 73.6%만큼 당뇨병 발병 odds(!=발병 확률)가 낮아진다
  - OR는 risk에서 한 개념 더 간 것이기 때문에 -> 1에서 멀어진 만큼 해당 질병 발병 오즈가 낮/높아지는 것이다.
  - 해당 질병 발병 확률의 낮/높은 RR이 판단한다.
- OR 해석 예) 흡연(위험노출여부O)을 하면, 안할경우 비해, (1보다 멀어진만큼인 0.7을 보고) CHD 발병 odds가 1.7 - 1 = 0.70 -> 70% 더 높다

문제는.. OR은 질병발생확률이 아닌 질병발생Odds의 비율차이가 난다는 것으로 알아라는 교훈

의연방03-1) 상관관계 측정

📜 제목으로 보기

✏마지막 댓글로

목차

Absolute risk

Absolute risk 계산 예제

질병과 위험요소의 상관관계 계산을 위한 Risk비교

RR & OR

Relative risk (RR)

RR 예시

Odds

Odds ratio(OR)

OR 수식정리

OR(Odds Ratio) 예시

RR vs. OR

Attributable Risk

Attributable risk (among the exposed) = ARe = risk difference (RD)

Attributable risk fraction (among the exposed) = AFe

AR, AF 수식 정리

Attributable risk 예시

Attributable risk for the population = ARp or PAR

ARp or PAR 공식

ARp or PAR 수식 정리

ARp 예제

RR vs AR, Af의 비교 예제

연습문제(RR, OR)

댓글 끝