의연방04) 컨파운딩과 상호작용
Confounding & Interaction(통추개념2,3)
📜 제목으로 보기✏마지막 댓글로
- 통계적추론 중요개념 3가지 중 나머지 2가지
- Confounding
- Interaction
- 정리하기
주요용어
-
Confounding : 위험요소(X)와 질병(Y) 둘다와 상관관계가 있으면서, 위험요소의 결과도, 질병의 결과도 아닌 변수
-
Interaction : X가 Y에 끼치는 효과가, 다른 변수 A값에 따라 달라지는 경우 X와 A간에 interaction이 존재한다고 말한다.
-
Additive model : 위험요소 X와 A에 둘다 노출되었을 때의 효과는, X에 노출되었을 때의 효과와 A의 노출되었을 때의 효과의 합이라는 모델
-
Multiplicative model : 위험요소 X와 A에 둘다 노출되었을 때의 효과는, X에 노출되었을 때의 효과와 A의 노출되었을 때의 효과의 곱이라는 모델
상관관계가 인과관계를 의미하지 않는다.
-
연구시, 상관관계가 발견되면,
-
이것이 진짜 상관관계인지 vs sampling error로서우연(random error)이나 잘못된 연구디자인에 의한 에러(systematic error, bias)인지 먼저 판단해야한다
-
-
상관관계가 진짜다 판단된 경우에는
-
상관관계->인과관계로 연결되는지 vs 인과관계가 아닌confounding 때문에 생겨난 -> 상관관계인지 판단해야한다
-
-
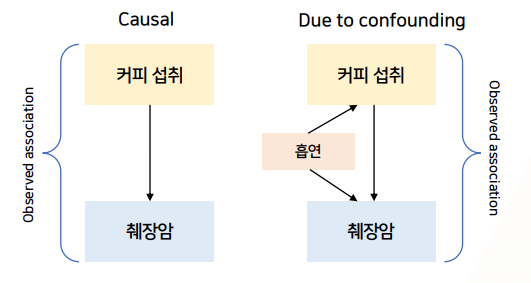
커피섭취-췌장암의상관관계 관측된 상태(진짜다)다 -> 2가지 설명가능한 상황(가능성)이 존재하게 됨.- 커피섭취가 -> 췌장암을 일으킨다(
인과관계가 있다) - 커피섭취가 -> 췌장암을 일으키진 않는데, 흡연이라는
confounder가 있어서2가지를 동시에 발생시키다보니,2가지가 상관관계가 있는 것처럼 보이게 만들었다- 흡연 -> 커피섭취 증가
- 흡연 -> 췌장암 증가
- (인과관계가 없음에도 불구하고,)커피 -> 췌장암 증가의 상관관계를 높였다.
- 커피섭취가 -> 췌장암을 일으킨다(
-
my)
- A -> B 상관관계를 보면, C->A, C->B의 Confounding을 생각하자
- A -> B 상관관계를 보면, Confounding생각후, 진짜 인과관계도 있으니 총 2가지 가능성을 생각하자
- X : 위험요소(risk factor) 또는 치료법 등 독립변수(설명변수)
- Y : 질병이나 질병으로 인한 이벤트 등 결과변수
- C : confounder
여기에서는 편의상 X, Y, C가 모두 이분형 변수인 예제를 사용했으나,
연속형 변수, 순서형 변수, 범주가 3개 이상인 변수들에 대해서도 모두 성립한다
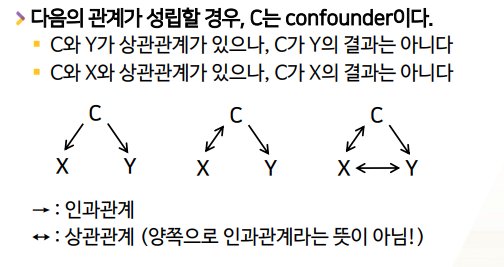
다음의 관계가 성립할 경우, C는 confounder이다.
- C와 Y가 상관관계가 있으나, C가 Y의 결과는 아니다
- C와 X와 상관관계가 있으나, C가 X의 결과는 아니다
즉, C가 x, y 모두와 각각 상관관계가 있으나, C가 x->c, y->c의 결과는 아닌 경우
- 가장 대표적인 경우가
C->X,C->Y의 인과관계인 경우다. - 또,
C = X 상관관계,C->Y의 경우도 있다. - 또,
C = X 상관관계,C->Y+X = Y 상관관계인 경우도 있다.
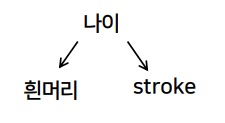
- X(독립변수):
흰머리-> Y(결과변수):stroke에 대해-
C -> 흰머리, C -> stroke를 일으키는confounder 나이를 생각해보자.흰머리가 많을수록stroke가 많을 수도 있으며 상관관계는 있는 것처럼 나타난다.하지만, 둘간의 인과관계는 없다나이라는 confounder가C->X, C->Y로 인과관계로 영향을 끼치기 때문에 보이는 가짜 인과관계(보이는 상관관계)이다.
- 그리고
X -> Y인과관계인 경우도 생각하자.
-
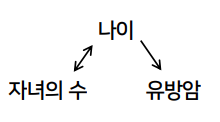
- X(독립변수):
자녀의수-> Y(결과변수):유방암에 대해-
C =상관관계= 자녀의수, C -> stroke를 일으키는confounder 나이를 생각해보자.자녀의수가 많을수록유방암가 많을 수도 있으며 상관관계는 있는 것처럼 나타난다.하지만, 둘간의 인과관계는 없다나이라는 confounder가C=상관관계=X, C->Y 인과관계로 영향을 끼치기 때문에 보이는 가짜 인과관계(보이는 상관관계)이다.
- 그리고
X -> Y인과관계인 경우도 생각하자.
-
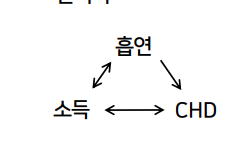
- X(독립변수):
소득-> Y(결과변수):CHD에 대해-
C =상관관계= 소득, C -> CHD, 소득=상관관계=CHD를 일으키는confounder 흡연를 생각해보자.소득가 많을수록CHD가 많을 수도 있으며 상관관계는 있는 것처럼 나타난다(소득은 모든 질병과 상관관계 있는 것처럼..많은 confounder가 운동/영양상태 등 존재).하지만, 둘간의 인과관계는 없다흡연라는 confounder가C=상관관계=X, C->Y 인과관계로 영향을 끼치기 때문에 보이는 가짜 인과관계(보이는 상관관계)이다.
- 그리고
X -> Y인과관계인 경우도 생각하자.
-
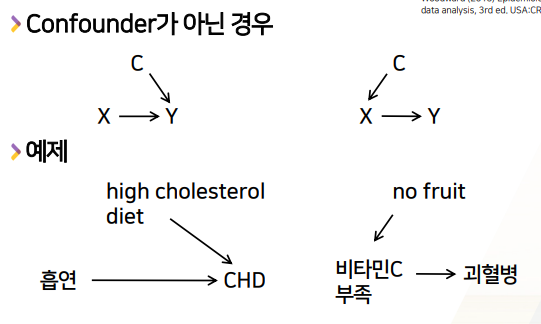
- C는 x와 y, 모두와 (상관,인과)관계가 있어야한다
- 둘 중에 하나와는 관계가 없는 경우, coufounder라 할 수 없다.
- high cholesterol diet는 X인 흡연과 상관(인과)관계가 없으므로 confounder라 할 수 없다.
- no fruit은 비타민C부족을 거쳐야만 괴혈병과 관계를 가진다. C와 y사이 직접적인 관계는 없으므로 confounder라 할 수 없다.
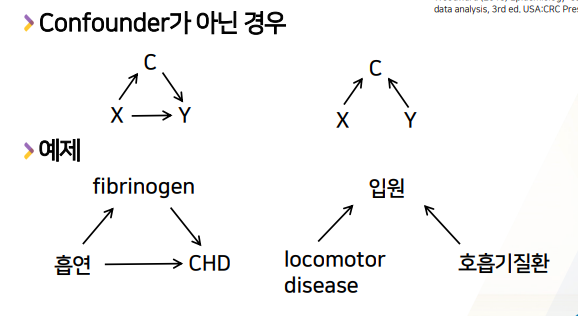
- c는 x or y의 결과여서는 안된다.
- x가 C에 영향을 끼치는 경우, C는 confounder가 될 수 없다.
- 흡연 -> CHD 영향끼치는 기전 중 1가지가 fibrinogen이라는 물질의 함량을 높여서 CHD에 영향을 준다고 알려져있는데
- x -> C가 성립하므로 C는 confounder가 아니다.
-
x -> C -> y가 성립하는 경우, 특별히mediate라는 용어를 쓰기도 한다.
-
- x -> C가 성립하므로 C는 confounder가 아니다.
- x:locomotor disease(운동기능장애)와 y:호흡기질환와의 상관관계를 본다고 할 때, 상관관계가 있는 것처럼 보일 수 있는데, C:입원이라는 factor때문에 그렇게 보일 수 있는데
- x가 있어도 C입원 할 가능성이 높아지고, y가 있어도 C입원 할 가능성이 높아져서 confounder처럼 x,y의 상관관계가 있는것 처럼 보이기도 하는데
- 근데, C가 x,y에 영향을 주는게 아니라 x,y의 결과 -> C가 된다면, 특별이 confounder가 아니라
collider라고 부른다.
- 근데, C가 x,y에 영향을 주는게 아니라 x,y의 결과 -> C가 된다면, 특별이 confounder가 아니라
- x가 있어도 C입원 할 가능성이 높아지고, y가 있어도 C입원 할 가능성이 높아져서 confounder처럼 x,y의 상관관계가 있는것 처럼 보이기도 하는데
- X, Y 둘 다와 상관관계가 의심되는 변수 C가 있을 때,
이 변수 C가 X의 결과가 아니고, C가 Y의 결과가 아닌 것이 확실하면 -> C가 confounder일 가능성을 염두에 두고연구를 해야 안전하다.
- 따라서
어떤 질병의 알려진 위험요소(risk factor)들은 모두 potential confounder이다 -
연령과 성별 역시 항상 potential confounder로 고려하는 것이 안전하다- 어떤 종류의 위험요소(X)도
연령/성별에 영향 안받기 힘듬 - 어떤 종류의 질병(y)도
연령/성별에 영향 안받기 힘듬
- 어떤 종류의 위험요소(X)도
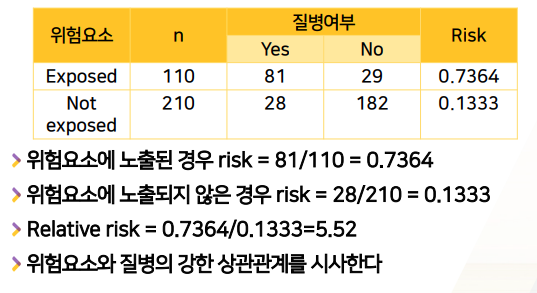
위험요소 - 질병과의 관계를 조사하였다.
- 위험요소노출O 110명, 그 중 질병O 81명
- (1) 위험요소 노출O의 경우의 Risk 계산 -> 81/110 = 0.7364
- 위험요소노출X 210명, 그 중 질병O 28명
- (2) 위험요소 노출X의 경우의 Risk 계산 -> 28/110 = 0.1333
- (3) 랠러티브 리스크(RR) : (1) / (2) =
- 위험요소 노출O의 경우의 Risk / 위험요소 노출X의 경우의 Risk = 0.7364 / 0.1333 = 5.52
- (4) RR 해석:
RR가 1보다 훨씬크다 ->위험요소 - 질병간의 상관관계가 강한 상관관계가 있다.- 왜냐면?
RR=5.52 -> 위험요소노출O의 경우, 질병O의 확률이 5.52배높아지기 때문
- 왜냐면?
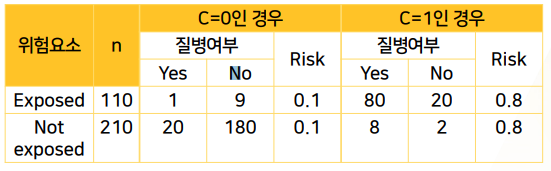

- (1) row:위험요소 노출O/X별 col:질병O/X의 행렬표에 더 높은레벨의 칼럼에
Confounder=0/1 (X/O)를 추가한다 - (2) C=0인 경우만 먼저, RR을 계산한다. (분모분자 다 바뀜)
- (2-1) C=0에서 위험요소 노출O의 Risk = 질병O/위험요소O = 1 / 1+9 = 0.1
- (2-2) C=0에서 위험요소 노출X의 Risk = 질병x/위험요소X = 20 / 20+180 = 0.1
- (2-2) C=0에서 RR = 0.1/0.1 = 1
- (3) C=1인 경우만 RR을 계산한다
- 80/80+20 (위O Risk) / 8/8+2(위X Risk) = RR = 0.8/0.8 =
- (4) C=0의 RR 과 C=1의 RR을 비교한다
-
(5) C에 따른 RR을 비교한 해석: `C에 노출되지 않은경우와 C에 노출된 경우, 위험요소-질병간의 상관관계가 1로서 없는 것으로 나온다.
- 노출O/x 각 그룹의 질병risk가 같다는 얘기로서, 위험요소가 질병과 상관관계가 없다고 나온다.
- confounder를 고려하지않고보면, 강한상관관계가 있는 것처럼 보였는데, confounder별로 따로 떼놓고 보면,상관관계가 없었다. -> 진짜는 상관관계없는 것
- 디자인단계에서 Randomize를 통해 confounder를 제거한다.
-
랜덤화: 각 연구대상자의 X값(위험요소노출 O/X 여부)자체를 랜덤으로 배정한다.- C가 되려면 x,y모두와 관계가 있어야하는데,
C->X로 가는 관계를 랜덤화로 끊어버려, c 성립조건을 없애버림
- C가 되려면 x,y모두와 관계가 있어야하는데,
-
매칭: 질병o와 질병x를 각각 표집할 때, 연령/성별과 같은 confounder들을 미리 비슷하게 맞춰서 뽑는다.C->y로 가는 관계를 매칭으로 끊어버려, c 성립조건을 없앤다.
-

- C=0, C=1처럼 각
Confounder값별로 스트레이라(Strata)를 따로 만들어서, 그 안에서 상관관계를 따로 따로 추정- 아까의 경우, 상관관계를 RR을 이용해서 따로 추정했었음.
-
-
strata별로 RR 추정값이 비슷하고, 전체 RR과 비슷하면 -> confounding이 없다고 생각할 수 있다.
- RR을 이용하거나 OR(오즈레이시오)를 이용해서 확인하면 된다.
-
strata별로 RR 추정값이 비슷하고, 전체 RR과 비슷하면 -> confounding이 없다고 생각할 수 있다.
-
-
confounder의 값별로 RR or OR이 많이 다르다 ->
interaction(인터랙션)이 있다는 뜻 -> interaction을 고려한 연구를 해야한다.
-
confounder의 값별로 RR or OR이 많이 다르다 ->
- confounder를 공변량으로서, 회귀분석안에 집어넣는 것
- 회귀분석의 설명변수로서 confounder를 포함시키는 것
-
회귀분석에서 나온 X의 회귀계수의 해석: 나머지 confounder들이 고정되어있을 때, 나오는 X가 -> Y에 끼치는 영향- 멀타이 베리어블 애널리시스 했다.(멀타이 배리어블 모델을 썼다.)
- 어저스티드 어날리시스를 했다.라고도 표현한다.
-
이 분석(confounder들을 설명변수에 넣은 회귀분석을 하되, 주 목적은 X->Y, 나머지 고정)에서도 X-Y상관관계가 유의하다면, X가 Y에 대한
independent effect가 있다(역학용어, 통계의 독립성과는 다름)고 표현한다.-
confounder를 공변량으로 넣은 어저시티드 어날리시스의 결과와공변량으로 넣지 않은 언어저스티드 어날리시스의 결과를 side by side로 나란히 보고하는 것이 좋다.- 본 독자가 직접 판단할 수 있게 된다.

- 본 독자가 직접 판단할 수 있게 된다.
-
- causal inference(코절 인퍼런스)라고 불리는 더 넓은 범위의 통계적방법론의 일부이다.
-
데이터를 잘 가공해서 -> X에 랜덤화를 적용시킨 것 같은 virtual data를 만들어 X-Y분석
- 나중에 다른 강의에서 소개

- 나중에 다른 강의에서 소개
-
없애는 것만이 능사가 아니다.
- 많은 경우 꼭 없앨 필요없다.
-
어떤 경우 이용을 할 수 도 있다.
- 예를 들어, X - Y 상관관계가 관측된 상황이라고 치자.
- X가 Y를 일으키는 인과관계는 없고, C라는 confounder에 의해 그렇게 관측될 뿐이다
라고 할지라도- 만약, C(confounder)가? -> my) Y가 관측이 굉장히 어려운 factor라면?
- 역으로 X를 이용해서 Y질병이 발생하기 쉬운 사람들을 찾아낼 수 있다???
- y질병고위험군을 찾기위해,
C땜에 생긴 상관관계라고 할지라도-> C덕분에 X를 이용해 Y를 발견할 수 있게 되는 것이다. - my) 찾기 힘든 y라면 -> C에 의해 보이기용 X-Y 상관관계가 생기고 -> X를 이용해서 Y 발견이 가능해진다. -> C가 만들어낸 보이기용 상관관계가 인과관계가 아니더라도 유용하게 쓰임.
-
confounding이 오류가 아닌 그 자체로 이해되어야하는 상황도 있다.
- X인종-Y심혈관계질환의 관계를 볼 때, confounder로서 비만도를 고려하게 되는데
- X아시아인 - C비만도 낮은 경향 + C비만도 - Y심혈관계질환과 관계가 있음 -> 비만도는 확실한 confounder임
- 그런데, C비만도의 효과를 제거하여 C비만도가 똑같은 아시아인vs백인을 비교해야할까?
- 강력한 confounder인 경우, C비만도가 똑같은 아시아인vs백인을 비교하는 것이 의미가 있을까?
- 아시아인은 백인에 비해 날씬하다는 것도 특성에 포함되고 bmi도 당연히 낮을 것인데, 이것을 굳이 보정해서 비만도를 동일하게 만들어놓고 Y를 비교할까?
-
강력한 confounder는, 있음을 이해하고, 고려해서 잘 해석하도록 해야한다.
- 고려안하고 해석하면 오류다!
- X인종-Y심혈관계질환의 관계를 볼 때, confounder로서 비만도를 고려하게 되는데
- 꼭 인과관계가 아니라 상관관계에서도 적용이 되는 개념
- 말로 설명시, 인과관계/이분형 변수를 setup해두면 더 쉬워서 가정함
- x,y,a 모두 범주3종류 이상 or 순서형 변수, 연속형 변수 모두에도 해당함
- 말로 설명시, 인과관계/이분형 변수를 setup해두면 더 쉬워서 가정함
-
인터랙션: x가 -> y에 끼치는 효과가, 타변수 A값에 따라 달라질 때,x와 a간에 interaction이 존재한다고 말한다.- 잘못 쓰이는 경우가 많은 용어다
- 인터랙션을 다른 말로
effect modification이라고도 하는데, a값에 따라 x가 y에 끼치는 효과가 달라지므로,a가 X의 효과를 modify한다라고 말할 수 있기 때문이다. - 또 다른말로,
heterogeneity of treatment effect(HTE)라고도 한다. x의 효과가 a값에 따라 달라지므로,x의효과가 a에 의해 나눠지는 그룹별로 hetero하다라고 말할 수 있기 때문이다.
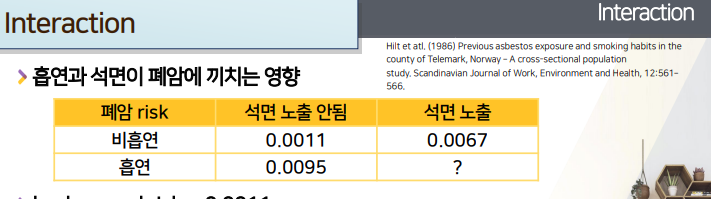
- 흡연과 석면, 2가지 factor가 폐암에 끼치는 영향을 보려고 한다.
- my) 일단 y에 대해 2가지 x후보군이 세팅되어있다 (둘중에 하나는 x, 하나는 a(interaion 일듯)
- my) 예제처럼 바로
확률인 risk를제시할 수도 있지만, 과제처럼만명당, 10만명당 incidence rate를 제시할 수도 있다.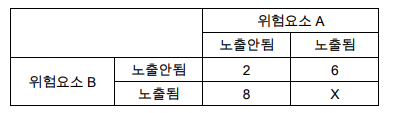
- my) risk는 이미 y(질병걸릴확률?)완료된 값 -> 2개 factor들만 row/column으로 가서 2by2 table로 표현되었다.
-
각 factor별 background(모든 위험요소노출X)에서 증가된 risk 구해놓기
- 2가지 위험factor(2 by 2)에 대해
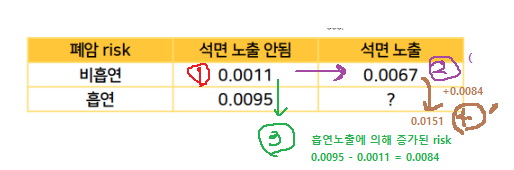
둘 다 노출이 안된 risk = background risk를 계산(확인)한다.- row 비흡연(위험노출X) && column 석면노출안됨(위험노출X) -> 0.0011
-
background risk를 기준으로 석면노출에 의한 증가한 risk를 석면노출O risk - 석면노출X risk의 risk차이로 계산한다.- background risk를 체크한 상태에서 row의 위험노출X를 기준으로 row방향으로 risk차이를 구하면, column에 있는 factor의 영향이 됨.

- background risk를 체크한 상태에서 row의 위험노출X를 기준으로 row방향으로 risk차이를 구하면, column에 있는 factor의 영향이 됨.
- 마찬가지로 column의 위험노출X를 기준으로 column방향으로 risk차이 =
흡연으로 인해 증가된 risk를 구한다
- 2가지 위험factor(2 by 2)에 대해
-
각 factor별이 아니라 2 factor모두에게 영향받을 때의 risk는?-
additive model로서 additive effect를 가정할 경우, 폐암risk는?-
background + 석면의영향(으로 증가된risk) + 흡연의 영향으로 계산한다
- 0.0011 + 0.00565 + 0.00.84 = 0.0151
-
이는, 비흡연일 때의 석면의 영향(+0.0056)이, 아래row의 흡연에서도 동일하게 영향을 미칠 것이라고 가정한 것 과 같다.
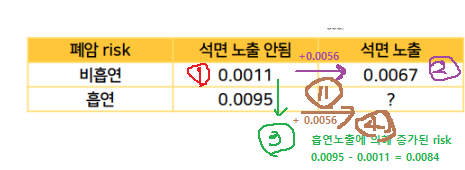
- 반대쪽에서 더해져도 마찬가지다. 이처럼 효과는 차곡차곡 더해질 뿐이니, 더해가면 된다는 것이 additive model이다.
-
-
하지만,
실제 risk는 0.0151보다훨씬 크다.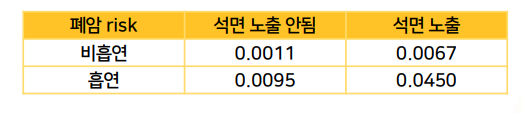
-
이 말의 뜻은
위험factor 2가지 동시에 노출되면, 각각의 효과보다 훨씬 더 나쁜 효과를 일으킨다는 말이다.- factor간에 시너지가 일어났다 =
interaction이 있다=석면의 효과가, 흡연여부에 따라 다르다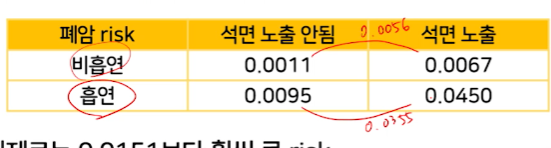
- 반대로
흡연의 효과가, 석면노출여부에 따라 다르다라고도 말할 수 있다.
- factor간에 시너지가 일어났다 =
-
이 말의 뜻은
-
- x축에 올라가있는
A값에 따라~X(legend)가Y(y축)에 끼치는 영향(2그래프 차이)이 어떻게 바뀌는지 보자.
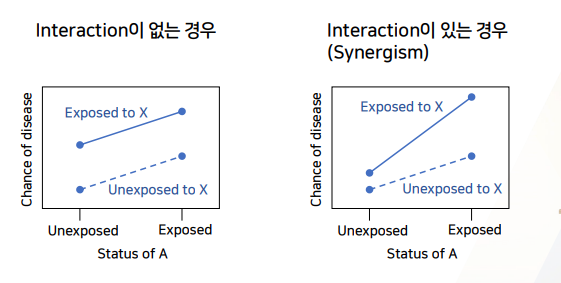
- 목적: interfaction을 일으킬
factor A값에 따라factor X가Y(risk)에 끼치는 효과를 나타내는 것- ~에 따른 변화 -> X축 -> factor A가 x축에 오게 된다.
y축: chance of disease = 질병이 발생할 확률 ->risk를 의미한다.x축: unexposed, exposed =예비 interaction 위험요소 A로서 노출X, O를 각각 나타냄legend로서 2개의 그래프:X->Y에 있어서 factor X의 노출X/O여부를 2개의 그래프로 나타낸 것
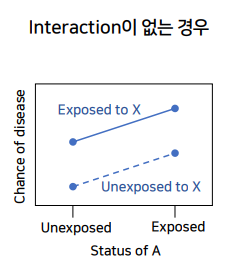
-
x축 1개 상황을 고정하여
위험요소A에 노출되지 않았을 때- 위험요소X에 노출되지 않았을 때 <-> X에 노출되었을 때 차이를 보고
X노출에 의한 Y risk증가 효과(차이)를 확인한다.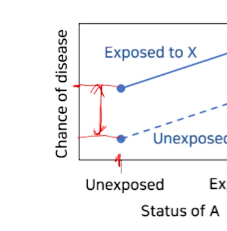
- 위험요소X에 노출되지 않았을 때 <-> X에 노출되었을 때 차이를 보고
-
x축 나머지 상황을 고정하여
위험요소A에 노출되었을 때의 ->X노출에 의한 Y risk 증가 효과(차이)를 확인한다- X에 노출되지 않았을 때보다, 노출되었을 때의 risk가 올라감을 확인한다.
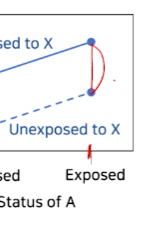
-
x축에 있는 예비 interaction factor A의 노출X/O에 따라
X에 노출X/O의 risk차이가 달라지는지 확인한다.-
(x축)factor A의 노출여부가X의 노출 X/O의 risk 차이에 영향을 주지않고 == 동일한 risk를 가져간다.- 즉, 인터렉션 그래프에서
x축에 있는 예비 인터렉션 factor A에 따라 risk변화가 나타나지 않으면==2개 그래프가 X축 여부에 따라 평행하면==인터랙션효과가 없는 것으로 판단하면 된다.
- 즉, 인터렉션 그래프에서
-
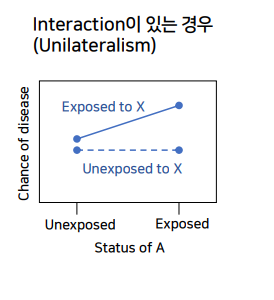
- 2개의 factor와 모두 만나면, 각각 노출되는 것보다 효과가 더 커진다 = interfaction이 있는 것
-
factor A에 노출되지 않았을 때-> 그래프차이를 보고 ->X의 Y risk증가 효과를 확인한다.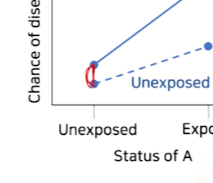
-
factor A에 노출되었을 때-> 그래프차이를 보고 ->X의 Y risk증가 효과를 확인한다.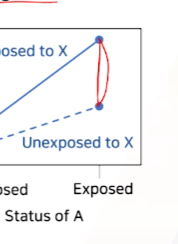
-
A 노출시X->Y risk증가 효과가더 많이 올라가는 것을 확인한다.- 평행하지않다 = 인터랙션 존재한다 = 시너지즘이 존재한다.
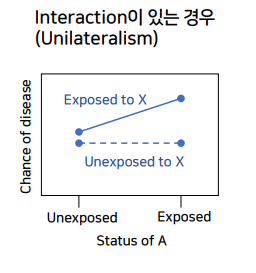
-
특별히 X축 1상황부터 보는게 아니라, legend 1상황에 대해 X축 2상황을 같이본다.
-
X에 노출되지 않은 경우에는, factor A의 y rist증가 효과가 전혀 없는 경우다
-
factor A 는 Y의 risk에 영향을 끼치지 않는 것으로 본다.
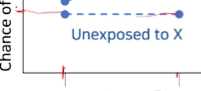
-
factor A 는 Y의 risk에 영향을 끼치지 않는 것으로 본다.
-
근데, X에 노출된 경우, A의 y risk증가효과가 나타난다.
- 차이가 일정하지 않다 = 2그래프가 평행하지 않다 = factor A(x축)에 의해 x->y risk 증가효과가 있다.
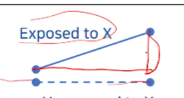
- 차이가 일정하지 않다 = 2그래프가 평행하지 않다 = factor A(x축)에 의해 x->y risk 증가효과가 있다.
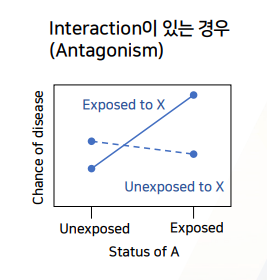
- factor A 값에 따라
X의 y risk증가효과의방향이 바뀌어버린다
-
먼저, X축의
factor A에 노출되지 않았을 경우를 먼저 보면, ->X에 노출되었을 때 risk가X에 노출되지 않았을 때의 risk보다 낮다- X에 노출되었을 때 risk가 더 내려간다? -> X는 y에 대해
protective effect가 있는 factor다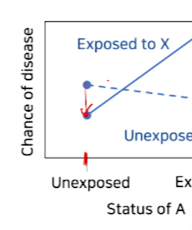
- X에 노출되었을 때 risk가 더 내려간다? -> X는 y에 대해
-
factor A에 노출된 경우,X에 노출되었을 때 risk가X에 노출되지 않았을 때의 risk보다 더 높아진다.- X가 y risk를 증가시키는, 나쁜영향을 주는 X라 볼 수 있다.
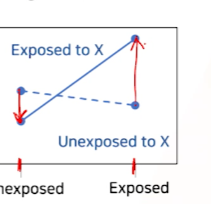
- X가 y risk를 증가시키는, 나쁜영향을 주는 X라 볼 수 있다.
- A값에 따라 x가 좋기도 했따가(y risk떨궈줌) or x가 안좋기도 했다가 하는 경우를
Antagonism이라고 부른다.
-
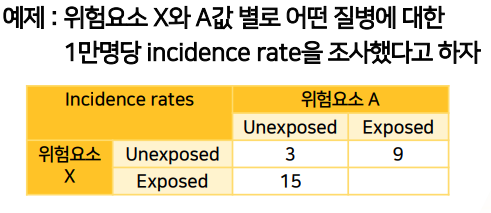
위험요소 X와 A 2개가 있다.
- interfaction 보는 문제인 듯?
- 위험요소 노출여부에 따라 1만명당 incidence rates를 조사했다.
- 앞에 문제들에선 risk(계산된 확률)이었는데, 여기는 확률이 너무 낮아서 10000만을 곱해 1만명당으로 줬다?
- incidence는 기본적으로
xxx명당 새롭게 발생한 환자의 비율이며, risk(발생확률)과 거의 비슷한 개념으로 생각한다.
- 일단 background risk처럼
2 위험요소 모두 노출되지 않았을 경우부터 확인한다. -> 3 -
background에서 위험요소A만 노출(->)될 경우를 확인 및 변화량도 확인한다- 3 -> 9로 위험요소 A노출시 (만명당) +6명 효과
-
background에서 위험요소X만 노출(↓)될 경우를 확인 및 변화량도 확인한다.- 3 -> 15로 위험요소 X노출시 (만명당) +15명 효과
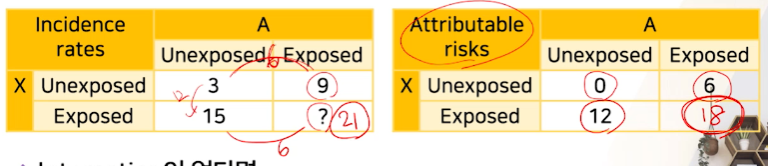
- 빈칸에 들어갈 값은? 만약 additive model이라면 한쪽에서, 다른한쪽의 증가량 더해주면 되는데

-
각 factor 노출시 변화량의 합 -> 둘다 노출시 변화량의 개념으로 보는 것 ==
Attributable risks로 보는 것- 둘다 노출되지 않았을 때가 기준이며, 0으로 만든다 ->
전체 -3 - 자동으로 위험요소 노출시의 값 =
변화량(증가량)이 된다. - 둘다 노출시
interaction이 없다면 단순 합으로 계산된다.- Attributable risks으로 보면 6+12 -> 18
- 기존표에서 보면, X부터 노출되었다 치면 3->15로 온 다음, A에 의한 증가량(+6)을 더해 15-> 21이 된다.
- 둘다 노출되지 않았을 때가 기준이며, 0으로 만든다 ->
-
각 factor 노출시 변화량의 곱 -> 둘다 노출시 변화량의 개념으로 보는 것 ==
Relative risk의 개념으로 본다.-
둘다 노출되지 않았을 때가 기준이며,
0으로 만든다-> 곱의 개념이므로 기준점을 1로 만드는전체 / 3을 한다
-
자동으로 위험요소 노출시의 값 =
변화량(배수개념)이 된다.- A노출시 3배 증가
- X노출시 5배 증가

-
둘다 노출시
interaction이 없다면두 변화량(배수)의 곱으로 계산된다.- 3배 X 5배 -> 총 15배
- 기존표 3 x 15 -> 45

-
addtive+multiplicative 의 계산은 interaction없을 때를 가정하고 2factor 모두 노출시의 값을 계산한 것이다. 실제 문제에서 주어지는 실제 값을 비교해서 차이가 나면 interaction이 존재하는 것이다.
- addtive model의 (만명당) incidenrate 계산 -> interaction없다는 가정하에 계산한 것
- ?가 21보다 현저히 높거나 낮으면 interaction이 있는 것으로 판단
- multiplicative model의 (만명당) incidenrate 계산 -> interaction없다는 가정하에 계산한 것
- ?가 45보다 현저히 높거나 낮으면 interaction이 있는 것으로 판단
따라서, 어떤 model을 가정하느냐에 따라서 interaction 존재 기준값이 달라져 판단이 달라진다.
- 실제값이 21이 주어졌다.
- additive 모델가정시 -> interaction 없네?
- multiplicative 모델가정시 -> interaction 이 있는데?
- 그럼 어떻게 model을 잡을까?
- 위험요소의 생물학적 작동기전에 따라 biological knowledge에 의해 결정되어야한다.
- 근데, 사실 addtive model을 사용하는 경우가 많다(직관적 이해가 쉬워서)
- 하지만, interaction 판단시, addtive model의 attributable risk보다는 RR, OR를 많이 사용한다.
- 그리고 RR, OR는 multiplicative model을 사용하는 것이 더 자연스럽다. 기본적으로 ratio는 더하기 빼기보다 곱하기 나누기 하는게 맞으므로
-
하지만, RR, OR에 log를 취하면, 자연스럽게 addtive model로 변하고, 그것을 이용한다

- 위험요소(X)와 질병(Y) 둘 다와 상관관계가 있으면서, 위험요소의 결과도, 질병의 결과도 아닌 변수를 confounder라고 한다
- confounder의 정의
- X와 Y간에 인과관계가 없어도 강력한 confounder가 있는 경우에는 X와 Y에 상관관계가 관측된다
- 이런 경우를 막기 위해 아래의 방법으로 confounding을 제거
- 연구 디자인 단계에서 confounding을 제거하는 방법에는 랜덤화와 매칭이 있다
- 데이터 분석 단계에서 confounding을 제거하는 방법에는 stratification, adjustment, propensity score analysis가 있다
- X가 Y에 끼치는 효과가, 다른 변수 A값에 따라 달라질 때 X와 A간에 interaction이 존재한다고 말한다
- Interaction의 종류에는 synergism, unilateralism, antagonism이 있다
- Additive model을 가정하느냐, multiplicative model을 가정하느냐에 따라 interaction 여부의 판단이 달라질 수 있다
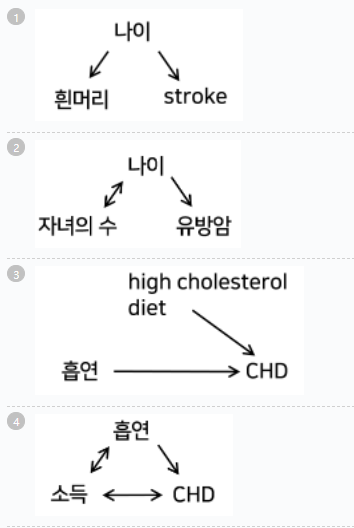
- 정답 : 3
- 해설 : high cholesterol diet와 흡연 간에 상관관계가 없으므로 high cholesterol diet는 confounder가 아니다.
- my) 일단 C가 결과가 되면 안되고, C는 x, y모두와 인과or상관관계가 존재해야한다.
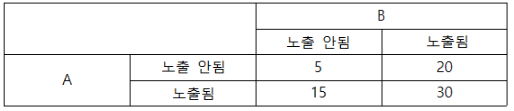
-
additive model을 가정한다면 A와 B간의 interaction은 없다.
-
addtive model을 가정한다면 A의 효과는 B에 노출되었는지 여부에 따라서 달라진다.
-
multiplicative model을 가정한다면 A와 B에 둘다 노출되었을 때 incidence는 만명 당 60명이다.
-
multiplicative model을 가정한다면 A와 B간의 interaction이 존재한다.
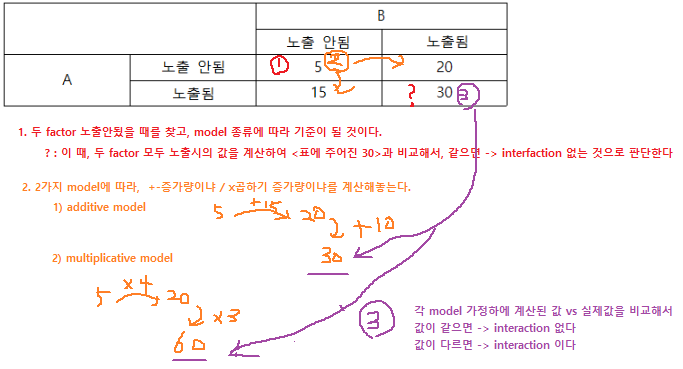
- 2번: addtive model을 가정한다면
A의 효과는 <B에 노출되었는지 여부에 따라서> 달라진다.= interaction인 존재한다는 말이다- 하지만, 계산값 30 = 실제값 30으로 ineteraction이 없다고 판단된다 ->
A가 어떤질병에 끼치는 영향이 위험요소B의 값에 따라달라지지 않는다
- 하지만, 계산값 30 = 실제값 30으로 ineteraction이 없다고 판단된다 ->
- 정답: 2
- 해설 : additive model을 가정한다면 A, B에 노출되었을 때의 위험은 5 + (20 - 5) + (15 - 5) = 30이 맞고, 이것은 interaction이 없음을 의미한다. 즉, A의 효과는 B에 노출되었는지 여부에 관계없이 일정하다.

